Astra
Giza
Cutout Corners



below image: G1 and S1
...viewed from the south
and facing roughly NNW 		liking the sphere, let's make it solid for a minute...
...and give it an... opaque, mirror surface texture...
hey... a mini pyramid appears... in the cut-out corner
i wonder, what angle
this reflection might
"create the illusion"
...of a flat sided...
...square based...
...mini pyramid ? 		i also happen to like that thin... wedgey... green triangle
...the long flat side is 60 cubits, same as distance to G1...
...but i wonder what the short side measures out to be...
...and what the implied hippo-angle is: square roots etc...
anyways, the cut-out corner... i made a little cubit-rod here
(below image) n now we're encountering familiar aesthetics
...above, i've made the sphere semi-transparent, but left the reflectivity... anyways
...from this distance, we can see it's about 47 (3 from 50): almost, but not quite
...and... zooming in, it looks to be... about 46... and... four fifths... or so...?
...also noticing: we have another familiar proportion right triangle...
and i wonder what all of the angles n measurements, in that one are
though the proper side is... whatever the point of G1-S1 intersection is
...maybe nothing... still, a valid question... something to keep in mind...
and don't mind the reflection, that's just camera angle (still, interesting)
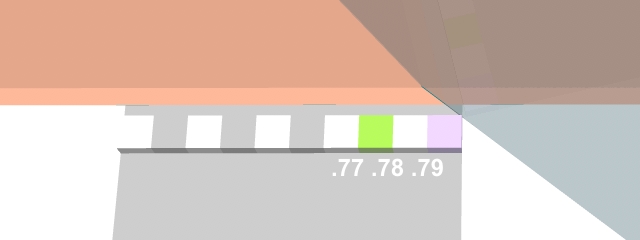
so now i duplicate a cubit rod group, and reduce by 10... for deci-cubits
...and reposition my new thingy... looks... to be... about... 46.78 or so...
and there are easier ways to measure things
...but i'm... demonstrating this... graphically...
repeating that process above, add a little color
n zooming in, ever closer... centicubits, now...
i've elevated the pyramid so the base is 0.02
...to match the top of the deci-cubit rod...
...the top of the centicubit rod is 0.03...
(its dimensions are... 0.01 x 0.01 x 0.10)
and this is at about maximum zoom, too 		...i can't get it any closer than that...
...i mean, i could explode everything...
...but anyways... this close, we can see
the plane of the pyramid's base is flush
but the slope falls short that same 0.01
the limit of the program... ok... 46.787
but: i can no longer attest to accuracy
...and again... this is where...
the disc of S1 meets the edge
of a G1 side... at ground level 		and, at this point, i have no idea what this number is sposedta mean...
playing with my calculator, i wanna see if i can get from zero to ~46.8
usin only "sacred" numbers n relationships like /2, /3, /5, pi, phi etc


addendum: there's gotta be a relatively simple geometric formula
already in common knowledge for determining that intersect point
...so, i ask around... a lil bit...
but, am met with only silence
...like if i don't know already
or how to look it up myself
i guess i don get to know
well, no one's gonna tell me
radius of S1 = 280 (height of G1)
sides of G1 = 440 ( 280 x 2 - 120 )
solve for the
Blue triangle
Blue + Red
Blue + Red x 4
Blue x Red
be creative
400 side ... 280 height
( 200 x 2 ) + ( 40 x 1 )
( 200 x 1 ) + ( 40 x 2 )



...ok, let's see what's goin on...
with the corner virtual pyramids
effectively cut-out from G1 by S1
...but first... i need to find out...
...what their... virtual height is...
...above image... view of G1 SE corner...
from the SE, G1 and S1 half transparent 		pink and blue measuring rods
show scale (1 cubit squares)
the shaded area is S1
green line is G1 east
blue line is G1 south
...each 2 cubits wide
...white dot is G1se
2 cubits in diameter
below left... back to the G1 SW corner
from the SW, at about 30 cubit elevation
...the peak of the virtual cuttout corner...
4 single cubit cubes, alternating green and red...
...for reckoning... top face elevation... is... 29.38...
the group coordinates are; (-196.9, 28.88, -196.9)
...here, can be seen just a teeny little corner of G1
peeking out, above the intersection of the 4 cubes
below right: view from SE: top face elevation 29.39
just the tiniest little speck shows, while rendering
which disappears at 29.40 (cube elevation 28.90)
also notice: the outer corners of the green boxes
just barely showing their points... so, we're over
but notice how jaggy the sphere edge is in both these images
(that's just because the S1 texture is set to half-transparency)
at this scale... those digital artifacts... are about... 0.07 cubits
...21 per cubit angle; and they disappear when set opaque...
you can guess how big the speck is... like 0.02 or something
...i could possibly zoom in closer; but, you get the idea...
in these next 2 images
i made the pyramid red
the sphere teal opaque
and the red cubes white
...in order to make the point of intersection
...just that much more apparent, in contrast
note the red speck in the center intersection
right image (and below image)
i've dropped the box down a cubit,
the top face elevation is now 28.39
...what we're looking at here is, basically
the underside of the previous reckonings
as they disappear into the pyramid walls
which are sloping downward to the SW
...this shows where the sphere S1
...continues its intersection with G1
at that same 1 cubit lower elevation
from the apex of the mini pyramid...
or, my rough approximation thereof
...at about: 196.9 cubits S and W
and below, i've turned a deci-cubit rod
45� to get somewhat sharper accuracy


aha: 0.65 (remember, from the short side of the green wedges)
...and not 2/3, not even close... well... within phi range...
but back to this 0.65
which reminds me of 130
...from where the LL line...
passes through the G1G2 box...
(between corners G1SW and G2NW)
...nearly bisecting at a 12:13 ratio...
immediately SW of this corner angle
and there's also elevation to consider
...the base of G1 is somewhat lower...
...than the rest of the arrangement...
the base of pyramid G2... is, actually
...at... about... this... elevation...
where S1 intersects G1 at the corners
n we'll look that exact figure up later
...but for now, let's get really precise
with this object set and camera angle


1st group coordinates: (-196.90, 28.88, -196.90)
2nd group coordinates: (-196.90, 28.89, -196.90)
new group coordinates: (-196.89, 28.90, -196.89)
...so, i've moved it in 1cc... both north and east...
and up 1cc (one 100th of a cubit or about 5.2mm)
1 cubit = 0.52375 meters, 52.375 cm, 523.75 mm
1 cubit = 20.620 inches or about 1.718333... feet
note: the "cc" i'm using here means "centi-cubit"
...not the common "cc" as in: cubic centimeter...
anyways, this new top face elevation is 29.40
(measuring half up from object center point)
(click pic for hi-rez)
...here... i've given both pyramid G1 and sphere S1 half-transparency...
the far white cubit begins to appear half-hidden, from inside the pyramid
...in the top image, you can see a little bit of white, meaning we're over...
and in the bottom image, a little bit of darker green, meaning we're short
you have to look at the hi-rez images (here, and here) to really tell, but
in the top (just-over) image, the green corners are sticking out a tiny bit
and in the bottom (just-under) image, they're just barely inside, even less
...so, in the general area... we'll round up... curve, anyways... anyways...
and at that height, that wide arc defines the square root of 2, for a cubit


...well, that's interesting... now that i know their height
...next, i'll put spheres on these corner cut-out pyramids...
that a sphere is making, exposing the outer halves of them
...those corners of G1... which are outside the volume of S1...


the Y coordinate altitude center of the transparent objects is 28.90 cubits off the ground
their dimensions each being 1 cubic cubit, add 0.5 to find the altitude of the intersection
28.90 + 0.5 = 29.40 radius from ground level... which gives us a diameter of 58.8 cubits
...which i... really just... so much want to round up, to a nice even 60 cubits diameter...
(from G1) the overhead cooredinates for the point of intersection is ( -196.89 , -196.89 )
that, rounding to 198, from 220 corner leaves 22 cubits... see the page about 44/45
...from 220, that 196.89 is 23.11
which, as the angle of a square
divided by the square root of 2
= 16.3412377132211132889...
times 2 would be 32.682475...
for the angle of a square corner
the pyramid that's being implied
ignoring ths sphere on the slope
...for the base of a square corner
double that 23.11 to 46.22 
here, i've made a corner pyramid
with a base of 33 cubits
and a height of 29 cubits
object center elevation 14.5

33 / 29 = 1.13793103448275...
which is very close to pi - 2
their difference, exactly, is...
2.0036616191070346177729882108657...

a rounded shortcut for pi (22/7) =
3.1428571428571428571428571428571...
and their difference, exactly, is...
2.0049261083743842364532019704433...
a little further, but by thousandths

looking back at the actual figures for a moment
23.11 x 2 = 46.22 square base
x root 2 = 65.364950852884453155614052832972

28.90
...here, i've made...
...a corner pyramid...
inside the G1se corner 		with a base of 46.20 cubits
and a height of 29.40 cubits
object center elevation 14.7 		and i had to make G1 half transparent
because the new little corner pyramid
is entirely inside, but right on the edge
liking that 14.7 cubit elevation
...i'll base my sphere on that...
29.4 radius and 58.8 diameter
G1 coords ( -196.89 , -196.89 )
here, i'll put a little cage around it
and the texture isn't perfect, aligned or proportioned
...but, this is just so you can get a rough, round idea 		here's another view
from the SSE of that
and here's a view of all 4 corners of G1
with little cutout corner spheres put on
(click pic for hi-rez)






Astra
Giza
Cutout Corners
� prev �
G1/G2 Square 		� next �
44/45