Astra - Giza

Lines

"The Chase Line" ...aka G1e-G3w
the midpoint of the east edge of G1
the midpoint of the west edge of G3

2000 cubits apart exactly and at exactly 45�
so, this is the first thing anyone should see

below image: lines between the 3 pyramids, from...
Clive Ross: Geometric Alignment of the Giza Complex
Topic 1: Linear alignment of the three Giza pyramids

the thick red line, which i label as G1-G3
is discussed on the Center Points page
but the thin purple line is G1sw-G3nw
notice where it crosses the G2 angle

(click pic for hi-rez)

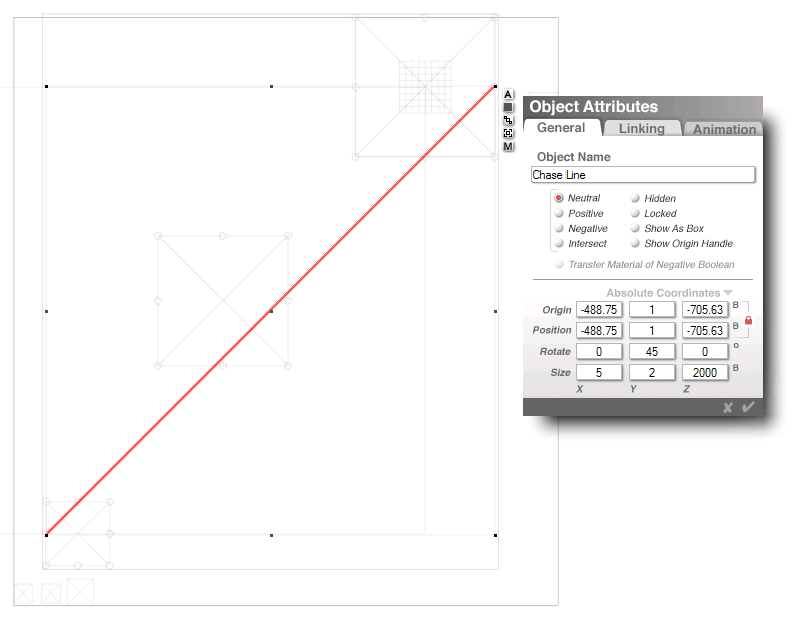
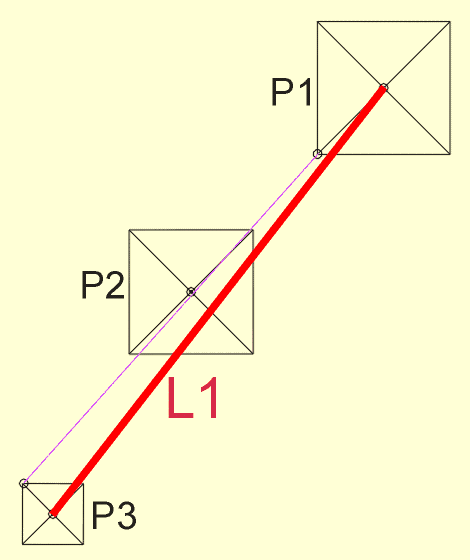
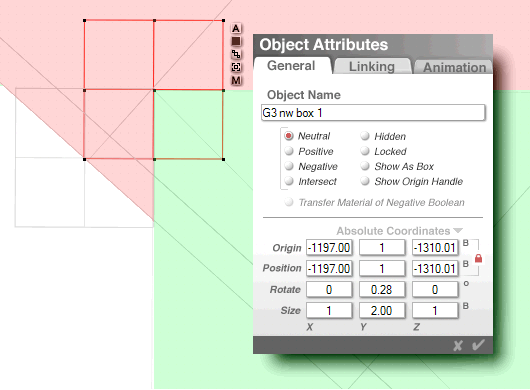
left image, the Chase Line (yellow)
and a new line: G1sw-G3nw (red)

G1sw = (  -220.00 ,  -220.00 )
G3nw = ( -1197.50 , -1310.50 )
         -1417.50 , -1530.50 )
mdpt = (  -708.75 ,  -765.25 )

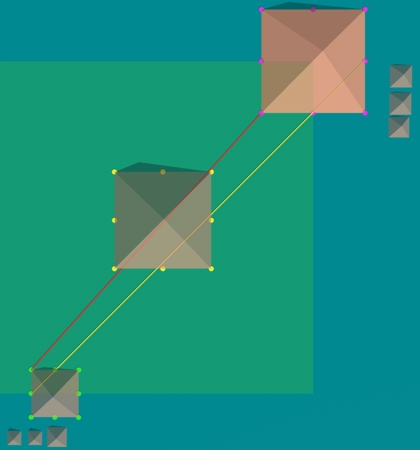
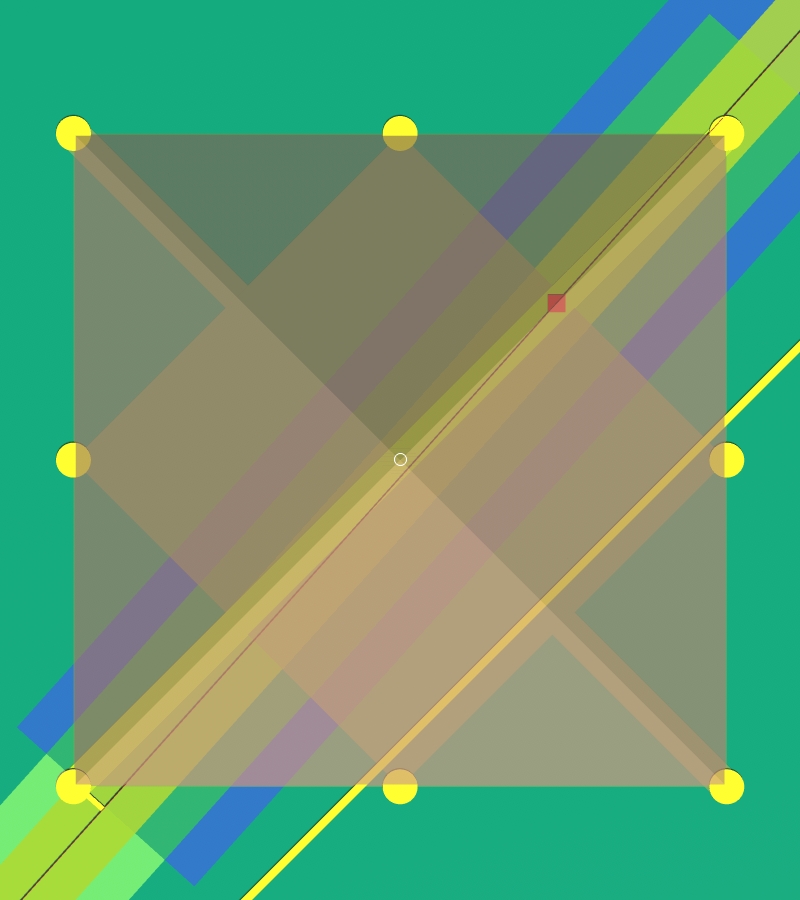
right image, wireframe overhead zoom on G1sw
(yellow dot) with line G1sw-G3nw (red, selected)

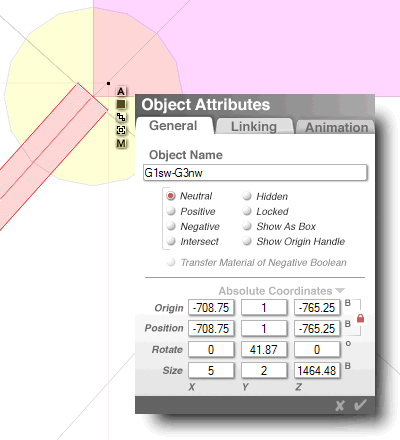
the object for G1sw-G3nw
measures 1464.48 cubits
and is rotated at 41.872�
which is 3.128� from 45�
which is 0.012 from 3.14�

1464.48 as 14, 64, 48
1400 plus 8 squared...
and then 6x8 over 100
...or, halved: 7, 32, 24
3x4/1000 > (8x4, 6x4)

left image: shaded wireframe
overhead zoom on G3nw corner
showing the line (shaded red)
extended to theory coordinates

remembering G3 is rotated 0.28� from that midpoint to G3nw actual G3nw* = ( -1197.00 , -1310.01 ) object = 1463.07 cubits at 41.87� distance = 731.535 (half object)
but 1463.07 as 14, 63, 07 2 and 9 and 1 multiples of 7	below image: red G1sw-G3nw from theory midpoint to G3nw actual

here, i've made a Phi measuring rod
(and placed it on top of G1sw-G3nw)
...the yellow line started out at 1618
...and the blue and green each 1000
...with the blue line off to one side...
...and the green line in the middle...

...i can now measure
...the phi proportions
...accurately enough...
between any 2 points
simply by resizing the
entire object group...

above image: the edge of the blue line on my phi marker
corresponds approximately laterally to the G2sw corner

below image: wireframe render composite zooming in on
the G2sw corner, with duplicated dot 7 cubits in diameter

...thus, phi of that line is lateral to G2sw...
that is to say, along that 1464.48 cubit line
starting from G1sw, and ending at G3nw...
phi (or 61.8 percent) of that linear distance
calculates as 1464.48 x 0.618 = 905.04864
(and behold, yet another interesting number)
stop when you get to approximately 905.04864
and you're within 3.5 cubits of the G2 sw corner
...where, precisely, is another interesting thingy

below image: i've placed a new "cube" object (red, selected)
perpendicular to the G1sw-G3nw line (lower left, doubled up)
just to see how far away it is from the SW corner of G2 (circles)
23.5 cubits long and 3.5 cubits wide... exactly 20 cubit difference

...so, following the numbers where they might possibly be leading
i could make the new line as 40 cubits wide, 20 cubits from center
...thereby respecting a dot at G2sw, being 7 cubits in diameter...

and it's phi, so rounding is close enough
...but now to move the G1sw-G3nw line
so that it touches both corners exactly

G1sw = (  -220.00 ,  -220.00 )
G3nw*= ( -1197.00 , -1310.00 )
         -1417      -1530
mdpt = (  -708.5  ,  -765 )

and i like both lines so this one's a copy 1463.77 cubits	multiples of 7 2, 9 and 11 2 + 9 = 11
and, where it crosses the G2 angle...

below image: maximum zoom overhead wireframe showing where the new line for G1sw-G3nw
crosses the sw-ne angle of G2, near the middle of the ne quarter, the red box is 1 cubit square

  45.00� 
- 41.87�
=  3.13�

3.13 is so close to pi
3.14159265358979323...
3.142857 142857... (22/7)
3.14... now i definitely want
to go back and remeasure
and see how 41.86� looks

back to G3sw
with the object
for G1sw-G3nw
(red, selected)
changed to 41.86�
(as 3.14� from 45�)
at various widths:
upper right 1.00
lower left 0.25
lower right 0.20

adjusting the new line that 100th of a degree
to make it 3.14� (for approximate pi) from 45�
...at that distance, offsets half of 0.25 cubits...
so 0.125 cubits... or, 1/8 of a cubit... exactly...
or tangent to a circle a quarter cubit diameter
or a 45� square measuring 0.88 cubits to a side

11.25� = 1/32 circle 
360 / 11.25 = 32
360 / 11.5 = 31.30434...
360 / 12.5 = 28.8

below: overhead rendering of G2
G1sw-G3nw (thin red line) is now
reset to 0.20 cubits wide at 41.87�

where it crosses the G2 sw-ne diagonal (red box)
is right between the G2 ne corner (upper right)
and the center point of G2 (white circle)

G2ne = (  -433.00 ,  -470.00 )
G2   = (  -638.50 ,  -675.50 )
 sum =   -1071.5    -1145.5
diff =     205.5      205.5
mdpt = (  -535.75 ,  -572.75 )

G2 side = 411
x root 2 (1.414)
angle = 581.24
for G2sw-G2ne
and G2nw-G2se

and G1e-G3w, aka
"The Chase Line"
(thick yellow line)

for a diamond
...inside G2...
G2 side = 411
/ root 2 (1.414)
side = 290.62...
for line G2n-G2e

...so, mathematically
the distance between
G2 center and G2ne is
half 581.24 or 290.62

half of that = 145.31
sequence, skipping 2
just as this line skips
the second or middle
of the 3 pyramids...

from the quarter point it is 6 cubits exactly
...to the point where the line G1sw-G3nw
crosses that 45� angle from G2's sw-ne...

above image: overhead of G2, the white dot is 12 cubits in diameter
below image: green dot added at G2 center is 15 cubits in diameter

the green dot marks G2 center, 15 cubits in diameter
the pink line is G1sw-G3nw and set at 0.2 cubits wide
the edge of line is actually tangent to the circle's edge

so the distance to the center of the line from G2 center
is actually 7.6 cubits perpendicular to the line at -48.13
...blue square marks the distance as about 0.3 cubits

as is common in measuring Giza
when i get one curious correlation
it tends to pop up again and again
more than once, even many times

in this case, there's 3.13� from 45�
with a tricky thing at an extra 0.01�
for a total of 3.14� for a pi to angle

...elsewhere, we've seen pi to cubits
other repeated interesting numbers
at unmistakably interesting angles...

Giza

Lines