 |
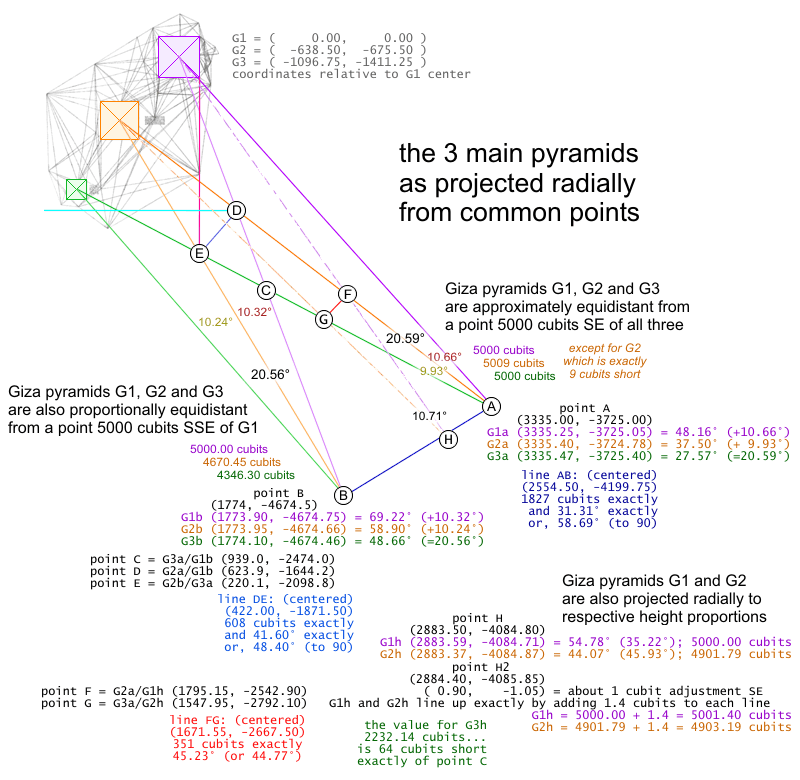
point A (equidistant) : (3335.00, -3725.00)
G1a = 48.16� + 90� = 138.16� (+10.66�) ; (3335.25, -3725.05) 5000 cubits
G2a = 37.50� + 90� = 127.50� (+ 9.93�) ; (3335.40, -3724.78) 5009 cubits
G3a = 27.57� + 90� = 117.57� (=20.59�) ; (3335.47, -3725.40) 5000 cubits
|
G2a = 37.50� + 90� = 127.50� (+ 9.93�) ; (3328.27, -3719.30) 5000 cubits
|
|
|
|
G1 = (0, 0)
G2 = (-638.5, -675.5)
G3 = (-1096.75, -1411.25)
|
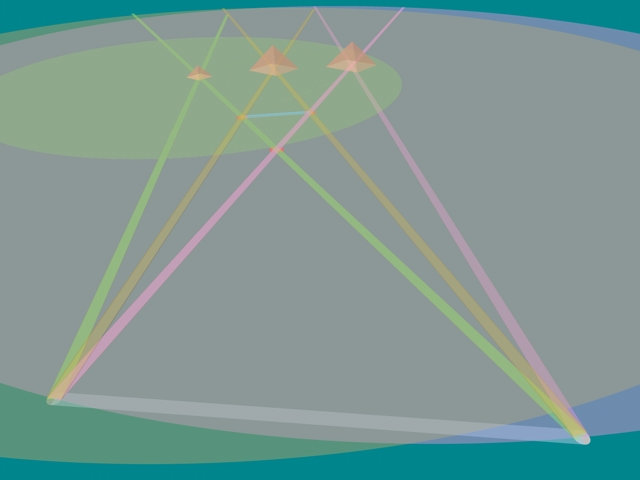
Giza pyramids G1, G2 and G3
are approximately equidistant
from a point 5000 cubits SE
|
|
|
in these images (above and below left)
...all lines are 5000 cubits exactly...
(from their respective pyramid centers)
|
|
|
gray dot is 55 cubits diameter
G1 coordinates: (3335, -3725)
(in cubits, SE of G1 center)
|
this is the intersect point
for the lines from G1 and G3
...while the line from G2...
falls about 9 cubits short
|
|
|
checkered squares are 1 cubit
(10x2) centered at dot center
|
red lines further divide cubits
into half measure quarter areas
|
|
|
|
|
|
...wide angle overhead perspective (above left)...
...lines from pyramid centers, 5000 cubits each...
rotated to intersect each other, at a common point
|
that same image above, overlay onto a Google Earth
satellite image of giza, and area SE (below left)
|
(below right) blue square outline area in above pic
far corner of a park area, surrounded on all sides
...by lush, well kept trees, to the north and west
...and several buildings, to the south and east...
|
|
|
 |
|
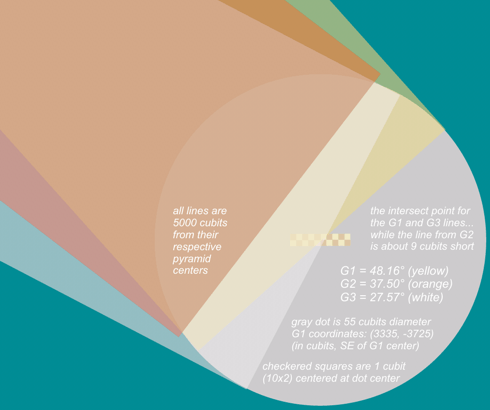 |
 |
...here's that zoom again (no wireframe)
(above and below dots do not correspond)
|
|
|
...ultra zoom, now... (curiosity)
...the legend says... 124 feet...
and that's as clear as it gets...
|
it looks like the outline of a guy
head, shoulders, and upper arms...
and not jus the trees to the west,
but the lighter ground to the east
|
|
|
29� 57' 42.00" N latitude
31� 09' 07.00" E longitude
|
for the latitude and longitude
the pointer is right between...
the upper center and upper right
square pyramid mound thingies...
and on the southern edge of them
...as measured from Greenwich...
|
|
|
|
|
so, G2 falls short a bit (by 9 cubits)
the SE equidistant point for G1 and G2
will be a bit to the southwest of that
and then the line from G3 will be over
|
|
|
...but maybe it's proportional...
...keeping the 5000 cubits for G1:
make the length of the line from G2
the same proportion that G2 is to G1
|
|
|
|
sides first...
heights later:
G1 = 440
G2 = 411
G3 = 201.5
|
(G1:G2) (411/440)
= 0.9340909090...
...interesting...
and times 5000...
= 4670.4545454...
|
x2 for my object
(centered on G2)
9340.90909090...
also interesting
9340.91 rounding
|
|
|
|
 |
point B (proportional) : (1774.00, -4674.50)
G1b = 69.22� + 90� = 159.22� (+10.32�) ; (1773.90, -4674.75) = 5000.00 c
G2b = 58.90� + 90� = 148.90� (+10.24�) ; (1773.95, -4674.66) = 4670.45 c
G3b = 48.66� + 90� = 138.66� (=20.56�) ; (1774.10, -4674.46) = 4346.30 c
|
G2b is proportional to G1b as
G2 is proportional to G1 side
these 2 new lengths intersect
at roughly: (1774.0, -4674.5)
|
|
|
now, working backwards
to find some relevance
for the length of that
...new line from G3...
|
5000.00 - 4670.45 = 329.55
4670.45 - 4346.30 = 324.15
total = 653.7
average = 326.85
|
|
|
G2b:G1b 4670.45 is to 5000.00
...as G2's 411 is to G1's 440
...(4670.45 / 5000 = 0.93409)
|
G3b:G2b 4346.30 is to 4670.45
...as what (X) is to G2's 411
(4346.3 / 4670.45 = 0.93059)
|
and 0.93409 to... 0.93059 is:
...1.003761... or 0.996253...
...ok, that's pretty close...
definitely within fuzzy range
but let's check the other one
|
G3b:G1b 4346.30 is to 5000.00
...as what (X) is to G1's 440
(4346.3 / 5000 = 0.86926)
no... that one's too far away
|
|
|
what would the ideal answer be ?
4670.45 x 0.93409 = 4362.6206405
4362.6206405 - 4346.3 = 16.3206405
...that's how much we're off by...
now that's... an interesting number
...16 x 2 = 32... and 32 x 2 = 64...
...the 4th, 5th and 6th power of 2...
|
|
|
...overhead zoom on point B:
with wireframe (above right)
...and without (below right)
|
|
|
|
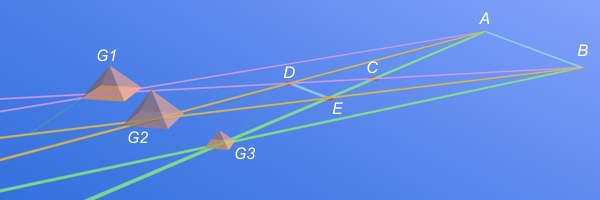
...Giza pyramids G1, G2 and G3...
are proportionally equidistant...
from point B (5000 cubits SSE G1)
based on the ratio of their sides
|
and again:
G1 = 440.0
G2 = 411.0
G3 = 201.5
|
G1b = 440.0 >> 5000 cubits (standard)
G2b = 411.0 >> 4670.45 = (5000(411/440))
G3b = 201.5 >> 4346.30 = (4670.45(411/440))+16
|
|
|
|
|
|
...and once again... point B...
(gray dot) = 55 cubits diameter
G1 coordinates: (1774, -4674.5)
(in cubits... SSE of G1 center)
|
|
|
...notice the point south from G1 center
is roughly the same as the length of G2b
(just an additional 4 or 5 cubits or so)
|
|
|
G1b = 4 and 3/4
G2b = 4 and 2/3
G3b = 4 exactly
|
|
|
|
object for lines G3a and G3b
are shown (left) centered at
and radiating from G3 center
"G3b" = 8692.60 total length
8692.6 / 2 = 4346.30
so its end points are
4346.30 cubits from G3
|
|
|
4346.30 / 5000 = 0.86926
4346.30 is 86.926% of 5000
|
441/440 = 0.93409090909...
squared = 0.87252582644...
|
|
|
G2 to G1... 411.. / 440 = 0.9340909...
G3 to G1... 201.5 / 440 = 0.4579545...
G3 to G2... 201.5 / 411 = 0.4902676...
|
0.45795... + 0.49026... = 0.9482221...
|
|
|
|
201.50 / 440 = 0.45795454545...
that x 5000 = 2289.7727272727...
that x (411/440) 0.934090909...
= 2138.85588842...
x 2 = 4277.7117768...
- 4346.30 = -68.588223...
of 4346.30 = 0.98421...
reciprocated... 1.0160...
|
201.50 / 411 = 0.49026763990...
that x 5000 = 2451.3381995133...
that x (411/440) 0.934090909...
= 2289.77272727...
x 2 = 4579.5454545...
- 4346.30 = 233.245454...
of 4346.30 = 0.94906...
reciprocated... 1.0536...
|
|
| |
|
G3 from an ESE perspective, radiating lines G3a and G3b (green)
|
|
|
 |
|
|
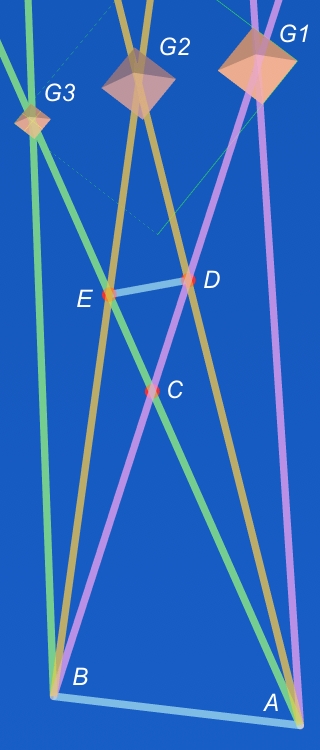
line AB (from point A to point B)
point A = G1G2G3a ( 3335.0 , -3725.0 )
point B = G1G2G3b ( 1774.0 , -4674.5 )
start point: 3335 -3725
finish point: - 1774 -4674.5
difference: = 1561 949.5
their midpoint: /2 780.5 474.75
from reference: + 1774 -4674.5
center of line: = 2554.5 -4199.75
|
i'm gonna call that one -4200 if i can
...and 2550, while i'm at it, possibly
(or... 2555 ...more likely, strangely)
|
|
|
1827.1 cubits
and -31.31�
or, 58.69�
|
|
|
1827 = 1800 + 27
(60.30) + (3.3.3)
|
608 = 600 + 8
60.10 + (2.2.2)
|
|
|
line AB centered
(2554.5, -4199.75)
1827.1 cubits exactly
and 31.31� exactly
or, 58.69� exactly
|
|
|
|
|
...perspective view of the whole thing so far... from high above and far to the WSW...
|
|
|
 |
|
line AB = 1827.1 cubits exactly
line DE = 608 cubits exactly
|
line AB = 31.31� (or 58.69�)
line DE = 41.60� (or 48.40�)
|
|
|
adjusting to (2550, -4200), it's:
1835 cubits and 31.18� to point A
1819 cubits and 31.45� to point B
|
adjusting to (2555, -4200), it's...
1826.5 cubits and 31.34� to point A
1827.7 cubits and 31.28� to point B
|
(so, maybe there's an arc involved)
|
|
|
|
 |
...and for the triangle connecting...
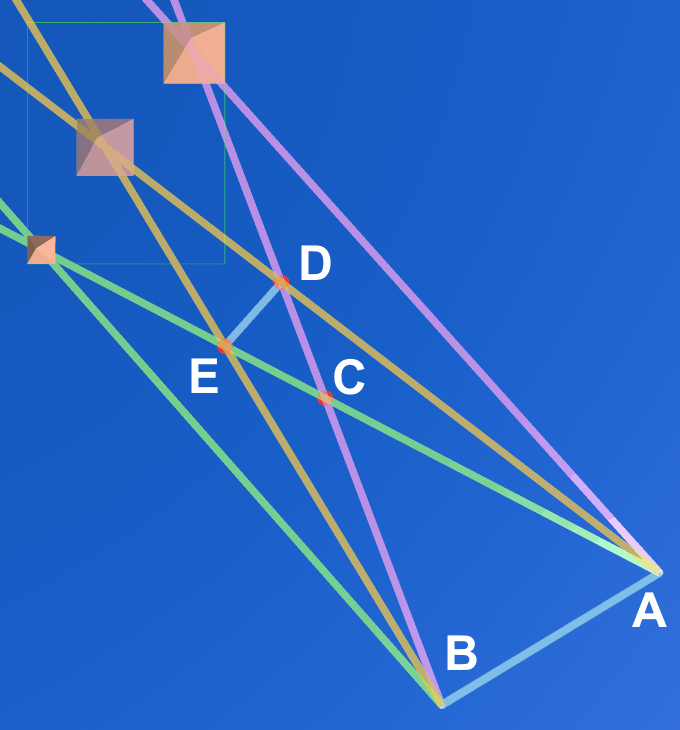
point C = G3a/G1b ( 939.0 , -2474.0 )
point D = G2a/G1b ( 623.9 , -1644.2 )
point E = G2b/G3a ( 220.1 , -2098.8 )
|
look at that point E
0.1 off from G1e and
1.2 off from 2100.00
(south of G1 center)
|
|
|
i also like the point C 2474.0 (cubits S of G1)
i'm sure there's something to all these numbers
|
|
|
line DE (from point D to point E)
point D = G2a/G1b ( 623.9 , -1644.2 )
point E = G2b/G3a ( 220.1 , -2098.8 )
start point: 623.9 -1644.2
finish point: - 220.1 -2098.8
difference: = 403.8 454.6
their midpoint: /2 201.9 227.3
from reference: + 220.1 -2098.8
center of line: = 422 -1871.5
|
|
|
line DE centered
(422.00, -1871.50)
608 cubits exactly
and 41.60� exactly
or, 48.40� (to 90)
|
|
|
|
looking at this picture
...i want to compare...
...lines AB to G1-G3...
|
|
|
line AB
1827 cubits
(3x600)+(3x9)
turned to 31.31�
and 31 x 12 = 372
12� over a circle
an additional 30th
...31 thirtieths...
1.0333... rotations
(reciprocal of 30)
(it's 30... of 30)
...special places
...special angle
...between them
|
|
|
|
G1nw-G3nw = 1816
G1nw-G3sw = 1989
average to 1902.5
|
G1e-G3w = 1000 root 2 = 1417.5
G1n-G3s = 1000 root 3 = 1732
G1ne-G3se = 1000 root 5 = 2238
|
|
|
G1-G2 = 929.5 at 43.39�
G2-G3 = 866.8 at 31.92�
G1-G3 = 1787.3 at 37.85�
|
|
|
G1-G2 + G2-G3 (arcing slightly)
929.5 + 866.8 = 1796.3 cubits
|
...average of their angles
(43.39�+31.92�)/2 = 37.66�
|
3.7 from 1800 (3.600), (6.300)
and 9 cubits from G1-G3, 1787.3
which is 12.7 cubits from 1800
|
add their angles together:
= 43.39� + 31.92� = 75.31�
...which from 90� = 14.69�
|
|
|
|
|
|
|
 |
...and now for the...
...3rd... dimension...
...oh, here they are...
...heights, in cubits...
|
G1 280.0 / 2 = 140
G2 274.5 / 2 = 137.25
G3 125.0 / 2 = 62.5
|
|
|
when i get the elevations of the pyramid peaks relative to each other
(they're not all on the same level) i can do more of a 3D projection
...and i would also need an elevation for the point of intersection
...but for now i'll just take those numbers as relative factors...
|
|
|
...so, putting them all on ground level... and...
using the same 5000 cubits... as a base reference
5000 / 280.0 = 17.857142857142857142857142857143
x (hG1) 280.0 = 5000
x (hG2) 274.5 = 4901.78571
x (hG3) 125.0 = 2232.1428571428571428571428571429
|
|
|
hey, wait a minute
did you see that ?
|
|
|
...start that bit over again... ok... 5000
over 280 = 17.857142857142857142857142857143
times 125 = 2232.1428571428571428571428571429
(i sense some sort of non-random significance)
...ok... i'm definitely using these numbers...
(see, cuz it's the same thing... but it's not)
|
what is: 280 to 125
...(7x40) (5x25)...
(7.2.2.5)...(5.5.5)
280 x 125 = 35,000
280 / 125 = 2.24
1/x = 0.44642857...
|
|
|
G1h = 5000.00 x 2 = 10000.00
G2h = 4901.79 x 2 = 9803.58
G3h = 2232.14 x 2 = 4464.28
|
let's see where they meet...
|
|
|
 |
and they don't...
aG3h is too short
it will never meet
the other 2 arcs...
...internalized...
|
|
|
however... aG3h is
just slightly over
the distance to G1
|
keep that in mind
for when i do the
vesicae for those
|
|
|
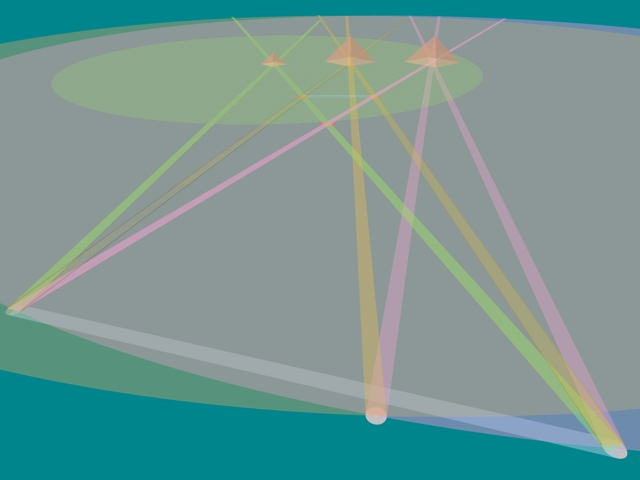
but, look where the other lines cross
...in this very wide overhead view...
|
in the NW, G3b ends right at line G2a
and SE... aG3h almost reaches point C
(and it's... 64 cubits short exactly)
...and it looks like G2b bisects aG3h
and to about the same radius for G1a:
|
...which i should look into, later...
it makes me wonder more about point C
(equidustance from other local lines)
|
|
|
|
 |
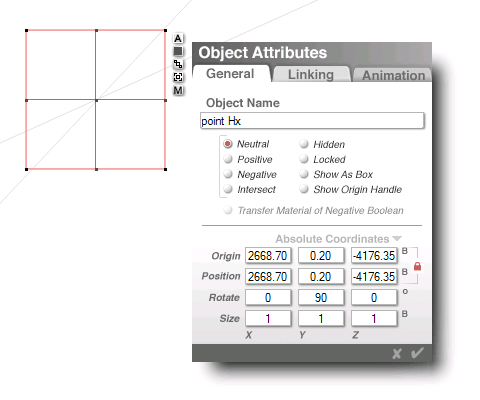
the halved 32nd angled sides
...of the 16 sided polygons
...their SE crossing point
...for arcs aG1h and aG2h
...is not far from there
...(2668.70, -4176.35)
|
|
|
 |
|
...where these new lines meet
for G1h, 5000 cubits at 54.78�
and G2h, 9803.58 turned 44.07�
point H = (2883.50, -4084.80)
|
|
|
 |
|
right next to the center point
for line AB (blue line, right)
looks close to phi proportions
|
...in fact, what i'll do is...
make a phi line... out of that
(duplicate object for line AB)
resize to 1618, duplicate that
resize to 1000, group together
resize to line AB length 1827,
(that stretched phi = 1129.17)
drag over, re-rotate to 31.31�
|
...close, but not close enough
...still, i'll make another...
there we go... and much better
|
|
|
the point of intersection
for points G1h and G2h is
phi of phi between points
A and B, parallel line AB
|
|
|
|
|
which is about 60 cubits away
or about 40 if it's an arc...
gray dot = 55 cubits diameter
|
|
|
and it's not exactly
phi plus phi, of phi
...or... something...
but it's close enough
...for me to notice...
...and notice it's...
...close... enough...
|
|
|
...and that's the line: AB...
i don't know what arc to draw
|
|
|
maybe it's already
just arc aG1-5000
|
|
|
points A, B and H
are all equidistant
from G1: 5000 cubits
therefore, they lie on
the edge of arc aG1-5000
G1a = G1 to point A = 48.16�
G1h = G1 to point H = 54.78�
G1b = G1 to point B = 69.22�
|
|
|
G1h = 54.78� (35.22�)
G2h = 44.07� (45.93�)
difference = 10.71�
|
|
|
|
...wireframe screencap image (right)
zoom on endpoints... for G1h and G2h
...when extended... an additional...
1.4 cubits...(height of G1 over 200)
...their ends line up... exactly...
|
G1h = 5000.00 + 1.4 = 5001.40 cubits
G2h = 4901.79 + 1.4 = 4903.19 cubits
...at coords: (2884.40, -4085.85)...
old point H = (2883.50, -4084.80)...
SE slightly ( 0.90, -1.05)...
|
|
|
|
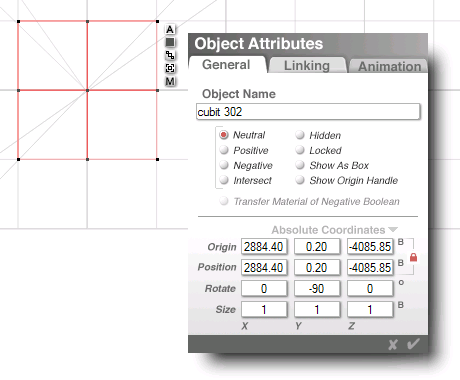 |
so unless there's something otherwise significant about 280
...or even if there is... we'll all keep our eyes peeled...
it appears the architects rounded G2 height 274.5 up to 280
...at this distance... nearest: 10... 20... 40... 70... 140
...but, divided by 100... that's the scale of this instance
|
|
|
so again, it's the proportional height of G2
relevant to the height of G1, to 5000 base x
...plus an additional 1.4 cubits for both...
|
|
|
|
2 more points to look into...
point F = (1795.15, -2542.90)
point G = (1547.95, -2792.10)
|
|
|
line FG (from point F to point G)
point F = G2a/G1h ( 1795.15, -2542.90 )
point G = G3a/G2h ( 1547.95, -2792.10 )
start point: 1795.15, -2542.90
finish point: - 1547.95, -2792.10
difference: = 247.2 249.2
their midpoint: /2 123.6 124.6
from reference: + 1547.95 -2792.10
center of line: = 1671.55 -2667.50
line FG center = ( 1671.55, -2667.50 )
|
|
|
line FG: (centered)
(1671.55, -2667.50)
350 cubits exactly
and 45.00� exactly
...ok... almost...
351 cubits exactly
and 45.23� (44.77)
...(being artists)
|
|
|
at first, i thought it was
...350 cubits... exactly...
...and 45.00� ...exactly...
|
|
|
|
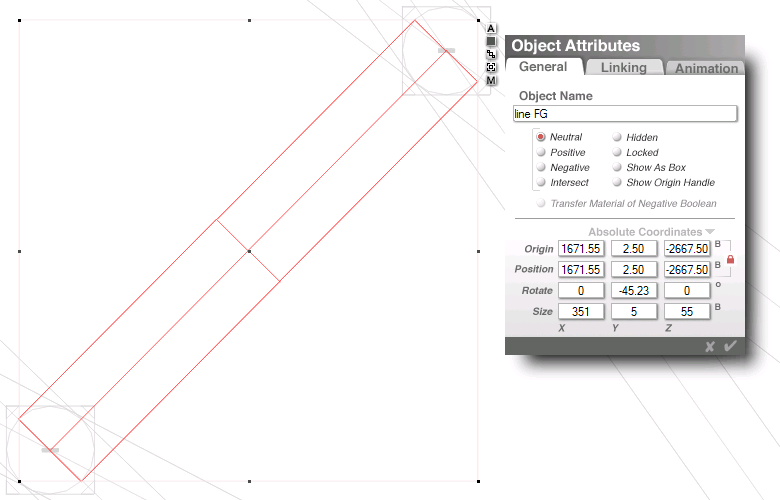 |
(remembering significance in the extra)
so what's the deal with the extra cubit
...reminds me of 280 and 125 earlier...
and i didn't think to just add together
...i'll do it now... 280 + 125 = 405...
... 400 + 5 ... 350 + 1 ... 750 + 6 ...
|
|
ok, here's that layout overhead diagram again,
so you don't have to scroll back up to the top
|
|

back to point A
...specifically
|
|
|
...now, these 3 lines...
don't all line up exactly
...but... where they do...
and intersect... is notable
|
|
|
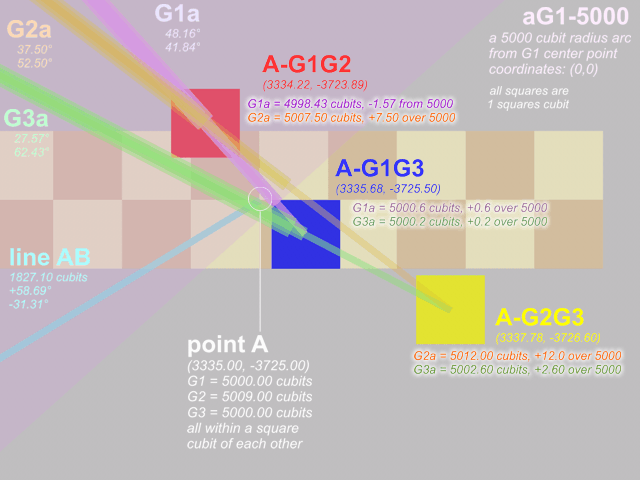 |
and again, point A: (3335.00, -3725.00)
all within a square cubit of each other
|
|
|
just NW of that (a couple cubits or so)
...where G1a and G2a actually intersect
...at point A-G1G2: (3334.22, -3723.89)
G1a = 9996.86 units, 4998.43 cubits, -1.57 from 5000
G2a = 10015.0 units, 5007.50 cubits, +7.50 over 5000
|
further to the SE (couple more cubits)
...where G2a and G3a actually intersect
...at point A-G2G3: (3337.78, -3726.60)
G2a = 10024.0 units, 5012.00 cubits, +12.0 over 5000
G3a = 10005.2 units, 5002.60 cubits, +2.60 over 5000
|
just to the SE (about one half cubit)
...where G1a and G3a actually intersect
...at point A-G2G3: (3335.68, -3725.50)
G1a = 10001.2 units, 5000.60 cubits, +0.60 over 5000
G3a = 10000.4 units, 5000.20 cubits, +0.20 over 5000
|
|
|
all squares are
1 squares cubit
|
|
|
and the squares (red, yellow, blue)
(or: line-pair intersection points)
don't correspond to Orion's Belt...
or to the positions of the pyramids
but they could define... an ellipse
|
|
|
|
|
...any 3 points... define a curve...
...the middle, as relative center...
...or... some other... incremental...
your eye gravitates to pixelization...
and estimates the outline of an object...
based on the information is has available...
...now... i'm not saying... there's an ellipse...
...implied here... at all... but, i... just made one...
|
|
|
 |
|



















