Astra - Giza - Center Points

Center Points

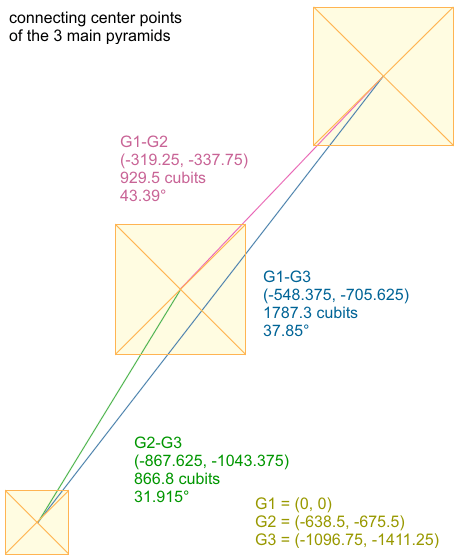
G1-G2: (-319.25, -337.75)
929.5 cubits, 43.39�

G2-G3: (-867.625, -1043.375)
866.8 cubits, 31.915�

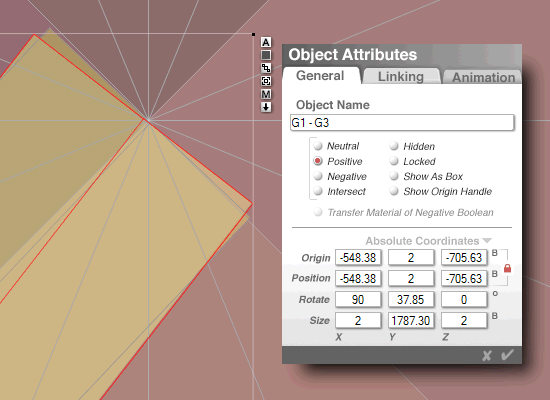
G1-G3: (-548.375, -705.625)
1787.3 cubits, 37.85�

coordinates (in cubits)
for the pyramid centers
(relevant to G1 center)

G1 = (0, 0)
G2 = (-638.5, -675.5)
G3 = (-1096.75, -1411.25)

G1 = (0, 0)
G1G2 (-319.25, -337.75)
G2 = (-638.5, -675.5)

G1 = (0, 0)
G1G3 (-548.375, -705.625)
G3 = (-1096.75, -1411.25)

connecting to G1 is easy to figure...
just divide the other numbers in half

but, connecting G2 to G3
requires some basic math

G2 = (-638.5, -675.5)
     (-......, -......)
G3 = (-1096.75, -1411.25)

     1096.75      1411.25
    - 638.5     -  675.5
    = 458.25    =  735.75
   /2 229.125  /2  367.875
    + 638.5     +  675.5
    = 867.625   = 1043.375

G2 = (-638.5, -675.5)
G2G3 (-867.625, -1043.375)
G3 = (-1096.75, -1411.25)

...so, they're going to be
hundreds of cubits long...
and probably at odd angles

and at this distance...
a hundredth of a degree
...is apparent, visibly

...a minute of arc is
...a 60th of a degree
...and bigger than a 100th
...by almost twice as much
if it were a 50th of a degree
it'd be exactly twice as much
...see, now you feel silly...

...anyways...
60 is to 100:
as 6 is to 10
and 3 is to 5
(6:10... 3:5)
..phi ratio..
...here, also

...a degree of a circle is
divided up into 60 minutes
...so, 1/10 of a degree...
is comprised of 6 minutes
one of those minutes is
one sixth of that, or
0.016666,,, degrees

base 10 decimal system
to a 360 degree circle

so that's the relationship...
six tenths... three fifths...

...60 x 60 = 3600
seconds per degree

a hundredth of a degree is ten sixths
or, five thirds of a minute of arc...
one and two thirds or 1.66... minutes
...further delineating... 100 seconds

...see how that works out...
(it reflects back on itself)
one hundredth of a degree is
...100 seconds (of a degree)

  (10/60)
x (10/60)
= 100/3600
or  1/36

line from G1 center
...to... G2 center
(-319.25, -337.75)
and 2 cubits wide

...43.39� and 929.5 cubits (exactly)...
...centers are off about a sixteenth...
(and that's... as close as i can get it)

and again... this is the design model...
the real pyramids are off more than this
or rather, the reference template is off
(to adjust other things more accurately)

above image is G2 center: at same 43.39�
...and it's off by the same amount as...
above right at G1 center: showing 43.39�
below right is G1 center: showing 43.38�

43.38� is off to the other side of center
by more than twice as much, and to the NW
...so, don't pay any attention to that...
...looks like it's probably about 43.387�

G1G2: 43.39 - 45 = -1.61
(phi, but it's degrees)

G2G3: 31.92 - 30 =  1.92
(phi plus pi, certainly)

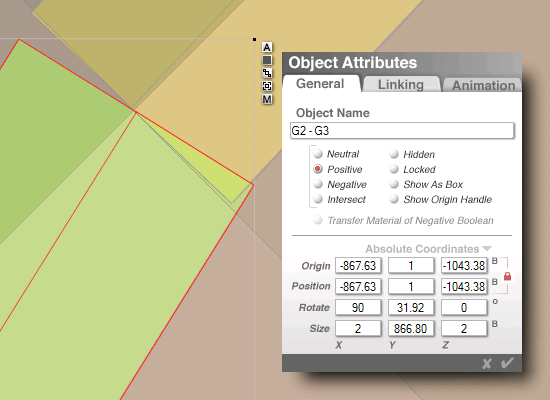...G2 center...
...to G3 center...
(-867.625,-1043.375)
again, 2 cubits wide
green line this time:
and it's even closer,
by about half as much

866.80 cubits... and
31.915� puts it even
with the G1-G2 line

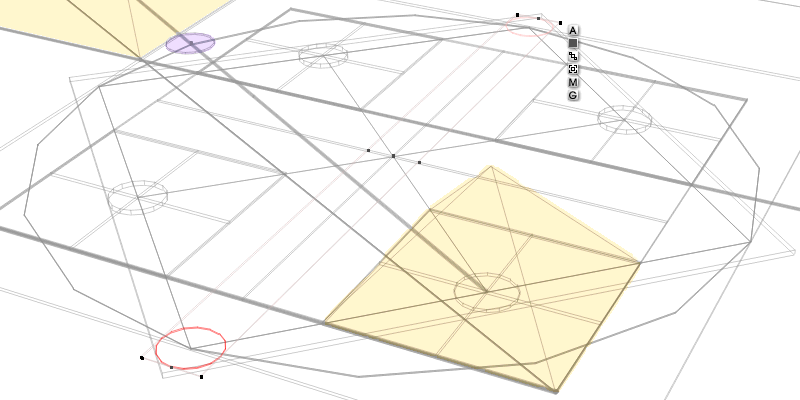
right image is at G3 center
below images are at G3 center

the purple dot is from the G3 rotator
(remembering there was some confusion
as to where, exactly... G3 should be)
 G3 = (-1096.75, -1411.25)
dot = (-1096.78, -1411.28)
(i left it in, to remember)

but look at this:
..(right image)..
..(blue circle)..
(in this program)
in wireframe mode
round objects are
represented... as
16 sided polygons
(so lucky for us)
the red G2G3 line
is shown crossing
the G3 rotator...
(where i left it)
right at a corner
at 1/16 clockwise
or 22.50� exactly

that other angled object:
(gray, unselected) is GPH
the grand plan hypotenuse
running from G1nw to G3sw
...and... notice where it
intersects the SE corner
of the NW mirror of G3
...(orange circle)...
not a coincidence...

...as discussed on page 1...
the circle's diameter is 707
...at coords: (-920, 1234.5)
nice easy number to remember

707/2 = 353.5
 -920 + 353.5 =  566.5
 -920 - 353.5 = 1273.5

...so i'll put some
new dots down at...
(-1273.5, -1234.5)
 (-566.5, -1234.5)

group, duplicate, rotate
...repeat until 16 total

(above) wireframe perspective view of G3 rotator: from above and southwest
(below right) overhead of same area: with complete group of 16 yellow dots
...the purple dot is the blue circle in the wireframe overhead (one above)
...and shaded purple in the perspective wireframe (upper left, just above)

(click pic for hi-rez)

NW square corner (below)
...at 55 cubit diameters
G3 and its guide squares
.each have a yellow dot.
..in their far corners..
.and flush to the edges.

in the wireframe image (below): the selected red outline is the G3 rotator
(which is 5 separate objects... grouped together to share a common center)
including the three 201.5 cubit wide G3 guide squares (thick red outline);
the 2220 circumference circle for their area (353.5 radius, 707 diameter);
and the 500 cubit wide square inside that circle, (turned 45� crossing G3)
...also: G3 (bottom, tan) and the 45� eighth dots (green), discussed above
...the 16th dots, however (blue 22.5�) flush to the edge of the G3 rotator
the rank-file limit of which being the 707 cubit circle (thin red outline)

double dot overlay (below right):
the first 16th clockwise from top
(upper right, above right image)
...at coords: (-784.72, -907.91)
just brushing the south edge of G2
with less than a 1 cubit overlap...
...remembering: G2 is 1 cubit south
from its basic design (see page 1)

source diagram for my "G3 Rotator" from:
http://goodfelloweb.com/giza/jlpamp.html

yellow 16th (-784.72, -907.91)
(55/2) 27.5 - 907.91 = -880.41
0.59 cubits overlapped into G2
G2's south edge at coords -881

the purple dot, now increased to 55 cubits
(at the same coords as the polygon corner)
also closely intersects the G2 south edge:

intersecting the G3 rotator arc
707 diameter at the G2-G3 line:
 purple dot (-783.68, -908.61)
(55/2) 27.5 - 908.61 = -881.11
11 hundredths of a cubit short
...works out to about 2 inches

...and again (as a marginal note)
the actual pyramids on the ground
are positioned slightly different
from the numbers i'm using... and
i'll look into that later, but...

the yellow dot: now removed...
and the purple dot: reduced...
to 2 cubit diameter (1 radius)
the width of the G2-G3 line...

...the red line (above) is the 16 sided polygon
the program displays as a circle object's edge:

and it doesn't line up exactly
but increasing the diameter to
2.50 cubits and rotated 11.25�
...the polygons' corners touch

and then i thought there was
something familiar about the
wireframe rectangle, for the
selected G2/G3 angle object:

just to check
real quick...
drag this pic
on the other:

it's Phi, a golden rectangle
cuz the gods made this place

...now i want to put that...
half root 5 radius circle in
...but what would that be...

as the short width (1) is:
EW cubits of G2/G3 centers
so Phi (1.618 of that) is:
NS cubits of G2/G3 centers

 G2 = (-638.5, -675.5)
 G3 = (-1096.75, -1411.25)

(X) EW G2-G3
1096.75
- 638.5
1x = 458.25

(Z) NS G2-G3
 1411.25
- 675.5
Phi = 735.75

side 1x = 458.25
x Phi (1.618...)
= 741.4640753...
- 735.75 = 5.714

so, a little off
...rounding down:
458 x 1.6 = 732.8
- 741.464 = 8.664

   8.664
+  5.714
= 14.378
 (-2.95)

14 and 3/8 cubits
...wiggle room...
and just guessing

so, a golden rectangle
with 1 as the side for
G3ns-G2ns... of 458.25
has a long Phi side of
458.25 x Phi = 741.464
...more than 14 cubits
longer than we need to
get north to G2 center

or, a golden rectangle
with Phi as length for
G2ew-G3ew... of 735.75
over Phi = 454.7185...

...so, i don't know exactly...
where, to place the centers...
(of the arcs i want to put in)
(i have to put them somewhere)

it might be rotated...
G3 is rotated slightly
...affecting G1nw-G3sw
...make that line wide

just: put in wide arcs
(make it... look nice)
...like a chalkline...
(taking consideration)
...neither Phi numbers
jumped right out at me
...like, i'd notice...

...a brassy rectangle:
458.25 x 735.75 cubits
centerd on same coords
as the G2-G3 connector
(-867.625, -1043.375)

and the center point is
half the EW G2-G3 (x/2)

and for EW coords, it's
due south of G2 center
...or, one half of x...

whatever the G2G3 distance is (EW)
make that square SW corner to G3sw
divide that in half, top to bottom
put the center points for the arcs
in each of the corners of that box
...half root 5... minus: half x...

the opposite arc naturally forming a vesica
...2 circles sharing the same common radius

...zooming back out again
(with all the objects in)
and just a rough overlay,
(rotated 180� from above)
but the half root 5 value
(small phi ratio side) as
defined by the green line
is crossing right through
circles 1 and 15 (of 16):
marking the outer edge of
the G3 rotator 555 circle

..rotator top..
...white dot...
 (-920, -881)

...orange dots...
(-988.96,-887.79)
(-851.04,-887.79)

each increased to
84 cubit diameter
(to be flush with
the smaller dots)

...yellow dots...
(-1055.28,-907.91)
(-784.72, -907.91)

...a difference of
270.56 east to west
each 135.28 from -920
(rotator's EW center)

G3: half root 5
...cyan line...
(-920, -907.91)

circumference of the 707 circle is 2220
the formula to find a circumference is:
2 pi times radius, or pi times diameter
... (2pi) x 353.5 = 2221.1060...
... (pi) x 707   = 2221.1060...

...so allowing for a...
similar margin of error
...the sum of the sides
of a (32 sided) polygon
...with 16 sides of 55
...and 16 sides of 84
(total all diameters)
...should be close...
... (16x55) + (16x84)
... 880 + 1344 = 2224

the 880 is interesting because:
the G2 south line is 881 cubits
south G1 center... coords (0,0)
but it was moved down one cubit
from 880 basic original theory
(see page 1 quotes on layout)

the orange dots almost touch the 500 side angled square (above)
but another 4 cubits in the diameter, and they do (below, left)
(an additional 2 cubit radius, the thickness of that cyan line)
bringing the total diameter up to 88 cubits... the radius to 44

880 = 2 x 440
... = 2 x 11 x 40
... = 600 + 280

but, i want to see:
if i can touch that
cyan line, again...

84 / 2 = 42
84 / 3 = 28
84 / 4 = 21

but 11.25� is going to be tough to split
yellow dots (5-8) are at the 45� angles
orange dots (9-16) are at 22.5� angles

(42 cubits) 11.25 / 2 = 5.625�
(28 cubits) 11.25 / 3 = 3.75�
(21 cubits) 11.25 / 4 = 2.8125�

...ah, 28 is even hundredths...
..good, that's the one i like..

taking the orange dots back to 84
and more duplication, rotation...

3.75� ...three, and 3/4...
...or one fourth from 4...

...again... white dot, at the top: (-920,-881)...
cyan line (-907.91): top corner of the 16 polygon
...big orange dot, at the 11.25� angle: (1/32)...

the purple and blue dots represent 1/3 of that:
the purple group is rotated -4.5� (total 6.75�)
the blue group is rotated + 4.5� (total 15.75�)

...tight zoom on just below the SW corner of G2...
...made GPH (G1nw-G3sw) orange, for distinction...
...all lines 2 cubits thick, yellow line is G2w...
the green line is the G2-G3 center point connector
cyan line marks the north 16 side polygon's corner

magenta line marks NS of center point
(through which passes the G2-G3 line)

and, this isn't exact:
the white dot, and its
yellow fellow 16ths...
are still 55 cubits...
2 of the 28 dots is 56
3 of the 28 dots is 84

so there's some wiggy proportional stuff goin on
...maybe i'll put some octagons etc in, later...

here's an overhead wireframe composite of the G3 rotator area
with the G1G3 connector put in, and selected (thick red line)
notice: it passes right through the center, of the north side
of the NE G3 rotator guide square (knew there'd be something)

(click pic for hi-rez)

the center of the G3 rotator (above):
the inner circle is 60 cubits diameter
the outer circle is 111 cubits diameter
both are just touching the 2 cubit lines
note the orange line in the upper left...
(that's the GPH line... from G1nw to G3sw)
...if i just make that one 4 cubits wide...
its edge would just touch that guide corner
...so now i'm starting to think these lines
do have a relevant width involved in their
relation to other things they touch...

...good guess... turns out
at 3.5 cubit width exactly
(left) the G1nw-G3sw line:
touches the corner exactly

...back up at G2sw (below image) i made GPH
4.5 cubits wide to touch the G2sw corner...
so it's projecting... probably to something
over by G1nw... which i'll look into, later

definitely something to that
(don't know... what, though)
...come back to it later...
that's the thing about giza
...everything i discover...
leads to something else...
cuz it's all connected...

so anyways, here's closeups
on the centers of G1 and G3
for the line connecting them
(red outline, selected object)

G1 = (0, 0)
G1G3 (-548.375, -705.625)
G3 = (-1096.75, -1411.25)

...as previously stated
and the object measures
1787.3 cubits at 37.85�

...i'm starting
to think of the
3 pyramids as
 G1 = father
 G2 = mother
 G3 = child

G2 being slightly smaller than G1
G3 being notably the smallest...
...and on the same land as G2...
...(G1 is on a lower foundation)
and then there's the satellites
...which i haven't got to yet

G1G3: 37.85 - 30 =  7.85
G1G3: 37.85 - 45 = -7.15
...HEY those differences
add up to 15, exactly...

in laying down the vesica,
i noticed that the 3 lines
projecting (NE) from G3...
while at different angles:
are equidistant, at G2s...

zooming in to measure
east from G2sw corner

...here, i've grouped:
color coded cubit rods
...in 10s and then 50s
(a pair is 100 cubits)

...four sets of five 10-cubit rods:
yellow, green, blue, red and orange

the 1st and 3rd 50 cubit bars are flush to G2s... and
the ones where the G3 lines cross are centered to G2s

the G2G3 line crosses G2s
at 77.5 cubits... exactly
...(from G2 sw corner)...

(above right) the line between the yellow and green
single cubit squares marks 160 cubits east of G2sw:
in maximum overhead zoom: looks like 159.35 exactly

77.5 x 2 = 155 159.35 / 2 = 79.675	411 - 77.5 = 333.5 411 - 159.35 = 251.65
...very close... so, where are these... projecting lines equidistant actually ?

create a new object, with
midpoint crossing G2G3...

...shaded bar
(above right)
is centered at
(-810, -950.75)
142 cubits wide
...so, 71 cubits
...center to edge

...if made 12.5 cubits wide,
north to south (lower right)
...it becomes flush with the
north edge of the G3 Rotator

...interesting, but...
...nowhere... nearby...
(for an east-west line)

...but, right at G2s...
where G2-G3 line crosses
and perpendicular to it
it's 65 cubits exactly
to either other line
...(below image)...

this new line is parallel to:
the root 3 vesica crossing...
reminding me how close to 30�
is that line from G2 to G3...

...just, slightly off, like that...
...reminds me of: magnetic north...
which is off from true north, a bit
and moves around a little over time
...so... i wonder where that was...
from giza, whenever it was built...
(might be one way to date the site)

G1G2: 43.39 - 45 = -1.61
(phi, but it's degrees)

G2G3: 31.92 - 30 =  1.92
(phi plus pi, certainly)

G1G3: 37.85 - 30 =  7.85
G1G3: 37.85 - 45 = -7.15
which add to 15, exactly

so here's the vesica for G2-G3...
here, i've drawn over the circles
and crossing intersector lines...
they weren't showing this high up

and you can see how wide they are
their common shared radius: G2-G3
= 866.80 cubits, turned at 31.92�

and of course, the circles cross
the G2 and G3 pyramid centers...
that's where they're drawn from:
the width, or height, of the eye

866.80 x 2 = 1733.6 cubits, diameter...
same as the NS distance of the pyramid area
from the north edge of G1 to the south edge of G3

the length of the eye, however...
the root 3 connector of the pair:
(cyan line) is about 1500 cubits,
same as "aG2sw-1500" (see page 5)
the distance from the G2sw corner
to outer edge of S1 (green line):
remember that 44�/45� connection,
remind me to make a vesicae of S1

866.80 x root 3 (1.732...) = 1501.341...
same as the radius of the arc "aG2sw1500"
a 3000 cubit diameter circle, which intersects S1

hypotenuse lines diagram from page 6
with new lines from this page in gray
crossing at perhaps interesting places

Giza

Center Points

^ up
Points

next �
Corner Points