Astra - Giza - Octagon

Octagon

wondering how octagons fit just so:
i'll make a template octagon object
as i've already done with a hexagon
and i could start from scratch, but
i want to maintain some continuity
 so, i'll just import that object
 and make an octagon out of that

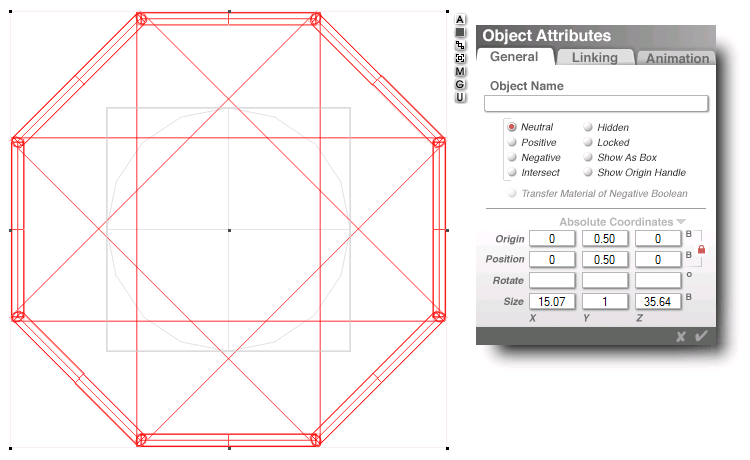
overhead, rendered wireframe composite
of the hexagonal object group i made...
full, selected red outline (below right)
...and a tight zoom of the far left corner
(below, far left) showing individual objects

again... here's my
hexagon worksheet
which is fun to 
just stare at...

so, in making an octagon from my hexagon:
using the same objects i have, already...
using the same textures, so they'll match
(and i can always change the color later)

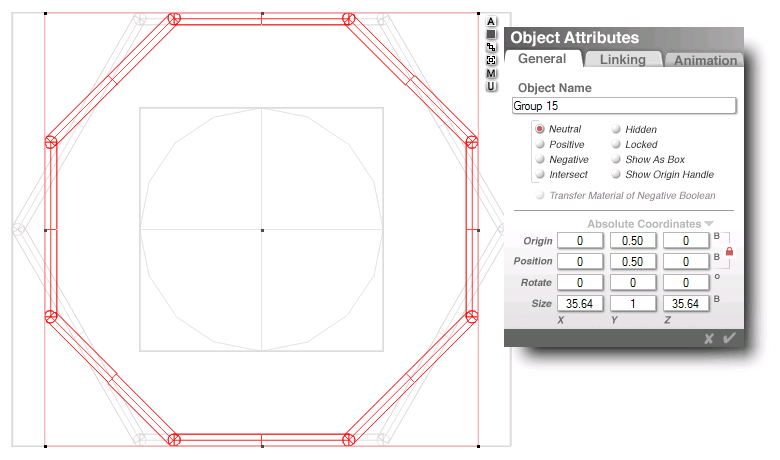
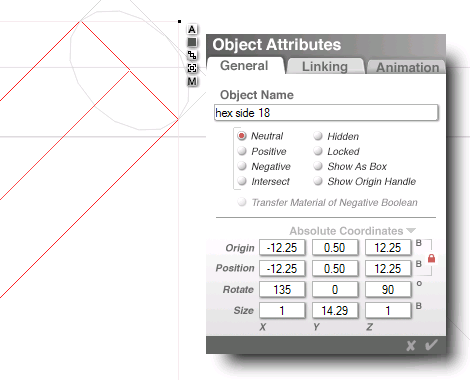
my hexagon object group
measures 41 x 35.64 units
...discounting the thickess
of the sides and corners...
which are each 1 unit thick
(twice one half, each side)
point to point, it measures
40 x 34.64 = 2 (20 x 17.32)

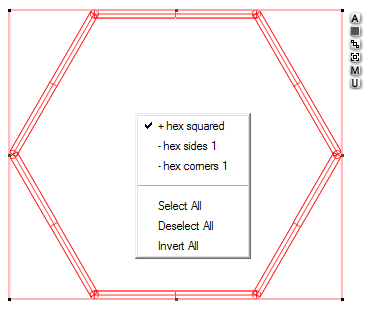i have it further grouped by sides and corners
to change those categorically, anytime (above)
but i'll just ungroup this whole thing (below)
...keeping only the top side and its 2 corners
...deleting the rest (they'll only confuse me)

so... just keeping the
2 corners and one side
from the hex object...

group those together, duplicate... and
put the new one negative Z from center
i now have 2 identical sides (as groups)
opposite center, positive and negative Z
each with 2 rounded corners (cylinders)...
and when grouped, together that's centered

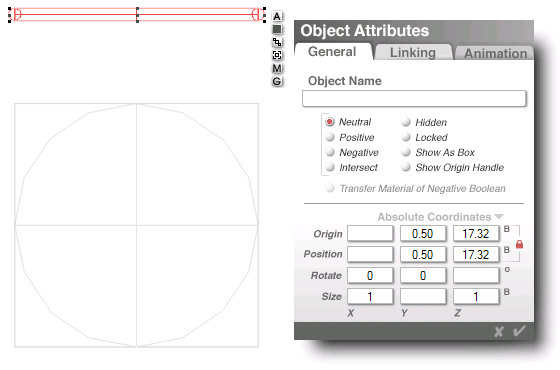
what remains, grouped together or not
...their mutual Z coordinate is 17.32

...that is: up, or north, from center
(as: the top side of a hex centered)

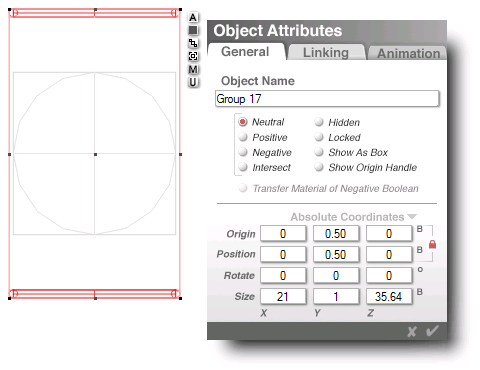
now, duplicate that group and rotate it 90�
group both of those, duplicate n rotate 45�
so, now i have eight sides, all centered...

and with twice as many corners as i need...
i'll delete the extras later, when i'm done

here's my octagon sides... but too long...
first, ungroup all of this... just once...
not to first level, of 8 individual groups
...or zero level, of individual objects...
...i want 4 pairs of sides, at 90� and 45�

select just one group and reduce its width
(below) until dots match top line of 17.32

the side's width remains one unit
only its length is being adjusted

...and it's still proportional...
with the dots being squashed here
what i'm aiming for is the center

and then there's this:
little freaky thing...
i almost didn't notice

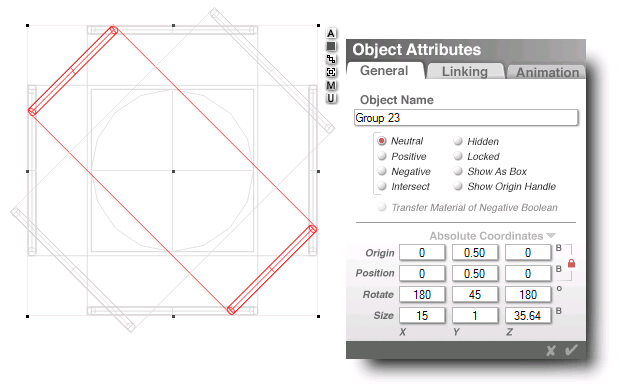
...see, it started at 21
...and i just reduced it
a couple units at a time

...it landed right on it
...at an exact even unit
so that got my attention

cuz i started with a hex
20 proportioned >> 17.32

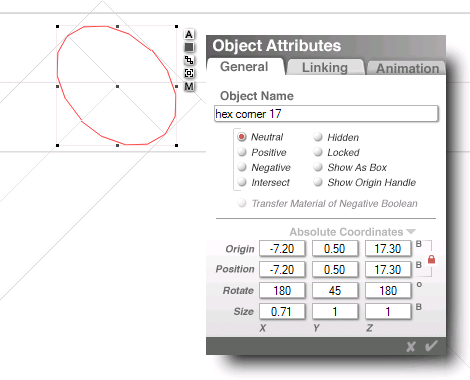
the line groups measure:
...15 units wide x 35.64

and the dot's new coords
...close: (-7.20, 17.30)
but my target is: 17.32

so that's interesting
...stumbled upon some
...basic, fundamental
...geometry, there...

proportional to the hex sides of: 20 x 1
but, with an additional 1 unit (2 halfs)
(for the radii, of the cylinder corners)
the actual side, point to point is 14.29

...and... just noticing: it's
close enough at an even 15...

which, in half, is 7.5
over 10 is 0.75 or 3/4

but that's the whole group...
see, the program is computing
the proportions automatically

...notice the polygon's
sides are still true...
16 sided, right edge on

...the dot is squashed to 0.71
which, i can only assume to be
rounded up from .707 sine wave
or anyways, close enough again

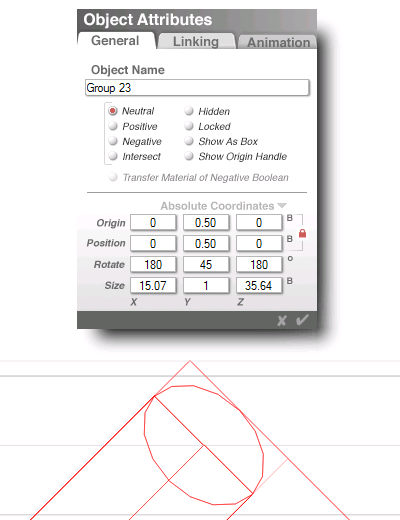so, back to the group, up from 15
stretching the group out to 15.07
puts the dot right on the line...
so, that would probably be 0.0707

ok, so now i select all 4 of these groups
and make them all that same 15.07 wide...
...they were, already, all still 35.64...

(17.32 times 2, plus 1 for 2 halfs thick)

this is where i ungroup everything down to individual objects
and return them all to their desired 1 unit width (diameters)

the circle and square are each 20 side to side
(to be even with the hex side, point to point)

so now i have an octagon
...made out of a hexagon
with the same proportions

so now, i can just group them together
and adjust them to any common diameter
...of any relevant arc, for comparison

done the normal way...
same process as before

just the corner dots this time:
grouped, duplicated and rotated

ungroup all those to zero level:
then regroup and rotate to 22.5�

no matter what i rotate them to
...their centers will still be
right on the circle edge line

but i want pairs with common coords
so i can put a cube line object in:

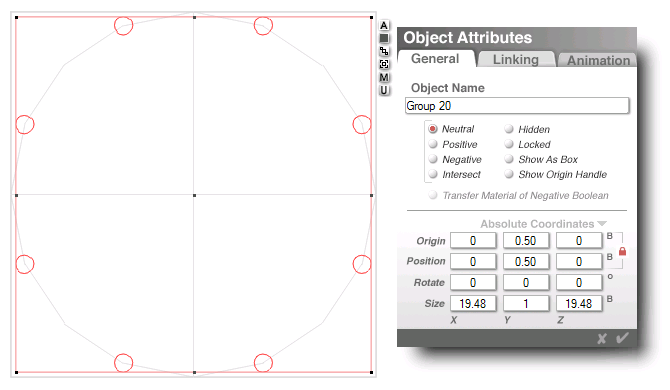
regrouped, the whole area is 19.48 square
that's how far the one unit diameter dots
approach the 20 side circle-square's edge
(at their angular displacement of 1/16th)

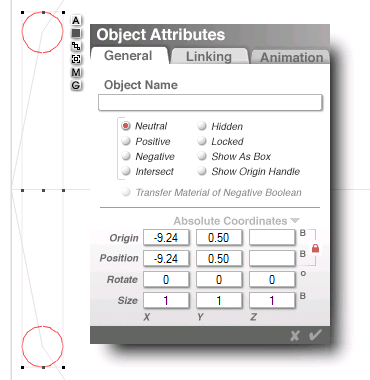the actual points, their centers
9.24 units... relative to center
and that's where i put the sides

length of the line between them
would be double that coordinate
...which... works out to: 18.48
...which is one less than 19.48
(the 1 being 2 halfs diameters)

...the other coordinate is 3.83
...the octagon's sides' lengths
being... double that... at 7.66

that 3.83 x 8 = 30.64
30.64 - 18.48 = 12.16
 and 12.16 / 4 = 3.04
for a 20 sided square

for a 10 sided square
...that would be 1.52

 for a 1 sided square
  that would be 0.152

 1/8 = 0.125
3/16 = 0.1875
5/32 = 0.15625
= 10/64 = 20/128
= 40/256 = 80/512

  0.15625
- 0.152
= 0.00425
x 4
= 0.017

 1/64  = 0.015625
 9/64  = 0.140625

 1/128 = 0.0078125
19/128 = 0.1484375

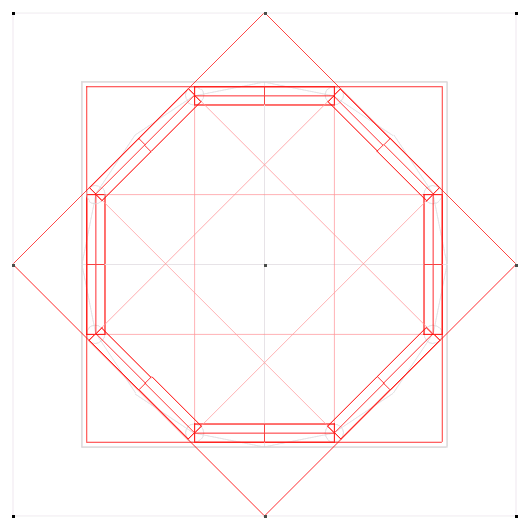
anyways, i put my sides in at 9.24
...and, each with a length of 7.66
repeat the aforementioned process:
...rename, regroup, retexturize...
...and now, compare to the circle:

but, what i have is not a common octagon
that we're used to seeing in a stop sign
(with sides flush to: up, down and side)
...this one is 20 units, from the points
so, the corners touch the circle's edges

...side to side it's only 19.48
...and minus 1 for 2 halfs each
for the thickness of the objects
makes it that same 18.48 distance
between the centers of the sides

all the dots in this image (above)
are centered on the circle's edge,
and all the lines are between them

now, if i wanted to do a regular stop-sign octagon...
i could start over and measure from the 10 unit sides
or i could just resize a duplicate of this to 21 plus

21 puts a side at 9,96
resize again to: 20.08
...rechecking the math
...the dots line up...
right exactly at 10.00

and their thickness has
been projected relatively
to a slightly exploded 1.08

...reset those to an even 1.0
...repeating the process with
a duplicated corners group...

...and here we have the regular
stop sign we're used to seeing:
...a large, or outer octagon...

these sides 
are centered
on the edges
of the circle
and the square

the half transparent pink and putple lines
are where you might expect (no surprises),
(1/16 of a circle relatively, or to 22.5�)
but the more solid maroon and violet lines
are rotated half, inbetween that normality
to an additional 11.25 degrees
(11.25 and 33.75 respectively)
...where their rounded corners
just touch, or: are tangent to
the inner sides of
the outer octagon

this is the kind of thing 
that's shown up occasionally
before in the geometry of giza

...lines not intersecting exactly
but when made a certain thickness...
they present as tangent to something

...now, again...
these are all 0.2
if i made them 0.3
they'd be tangent to
each others' centers
...agd again, that's...
outer octagons 20 sides,
inner octagons 20 corners

so, an octagon, at that 3/4 turn,
is demonstrating the 3 internally
...locking on to it, at the curve

the 3:4 ratio is natural for an octagon
the 4 in this case being the sum of the
2 objects, corner and side, 0.2 each...

...very celtic, very spirograph:
...even wth the different colors
it's hard to tell where one line
ends, and another keeps going...

almost as if that's what it is...
it's just naturally demonstrating
an inherently incremental spiral:
like the golden mean or a fractal

and where it's not "exactly" exact
...is because it's not a circle...
it's a square'd off version of one
...or a square's... version of one

or it could also be said to be
a circle's version of a square

the octagon is as a landmark or signpost
...inbetween... a square and a circle...

in this one (above), with just 2 outer octagons
...the solid blue and green octos are normal...
and in the one (below), adding 2 more octagons:
the paler blue and green being: 11.25 and 33.75

and we could do this all day
(until we ran out of colors)
...a natural infinity mirror

proportionally accurate
only the scale projects
(inward and/or outward)

with their relative value to each other
being their common phase of interest...
and their lateral counterparts, sharing
similarities... reflectively relatively
...this thing measures stuff for you...

handy thing to have around
...save that object group:
move on to the next thingy

Giza

Octagon