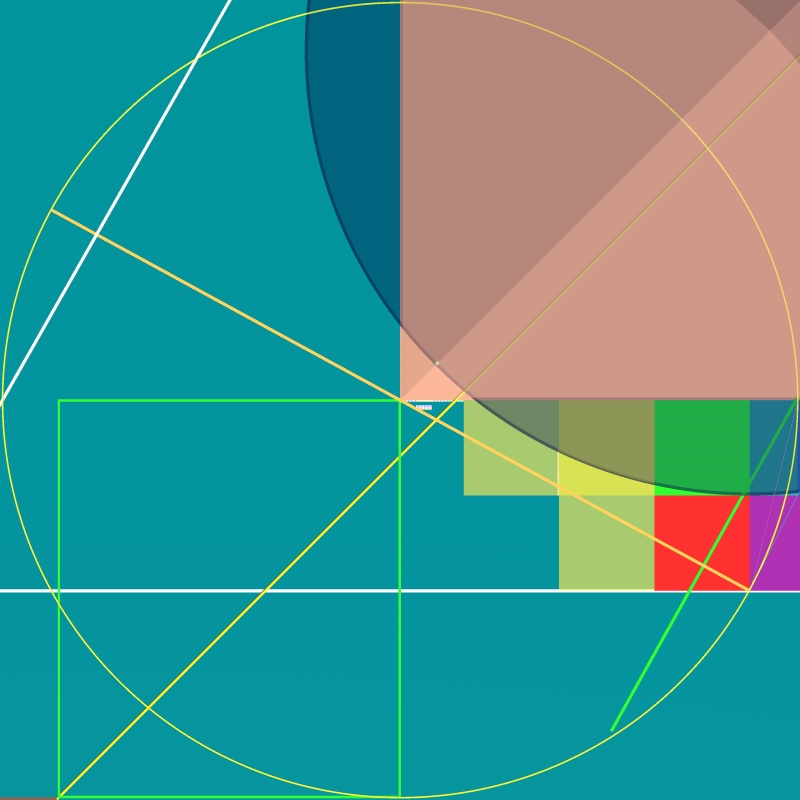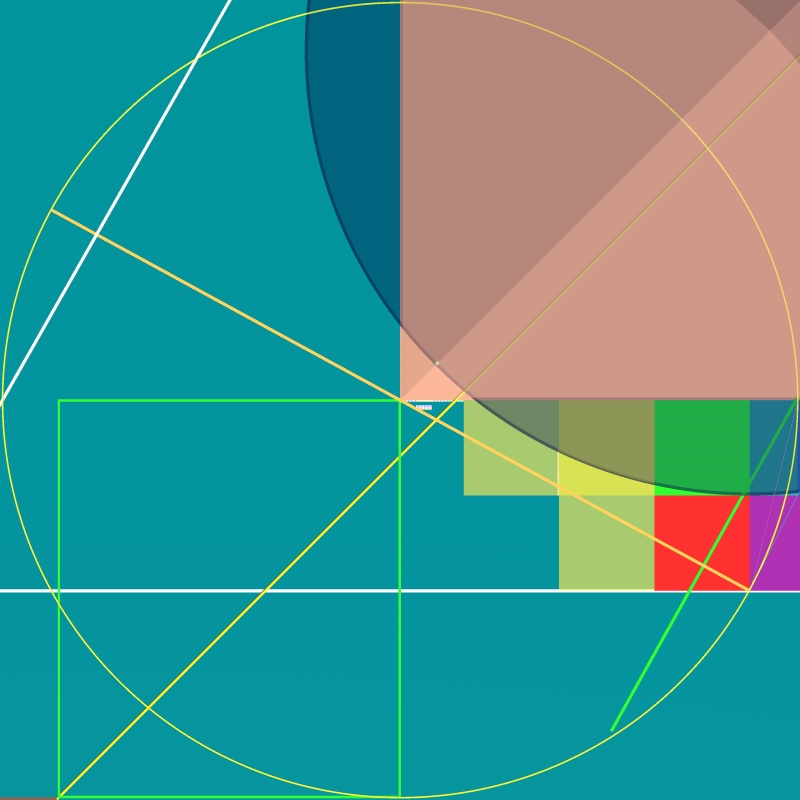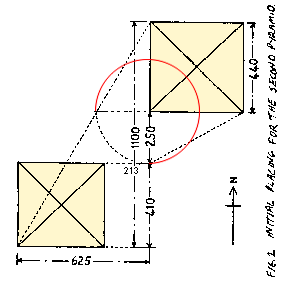
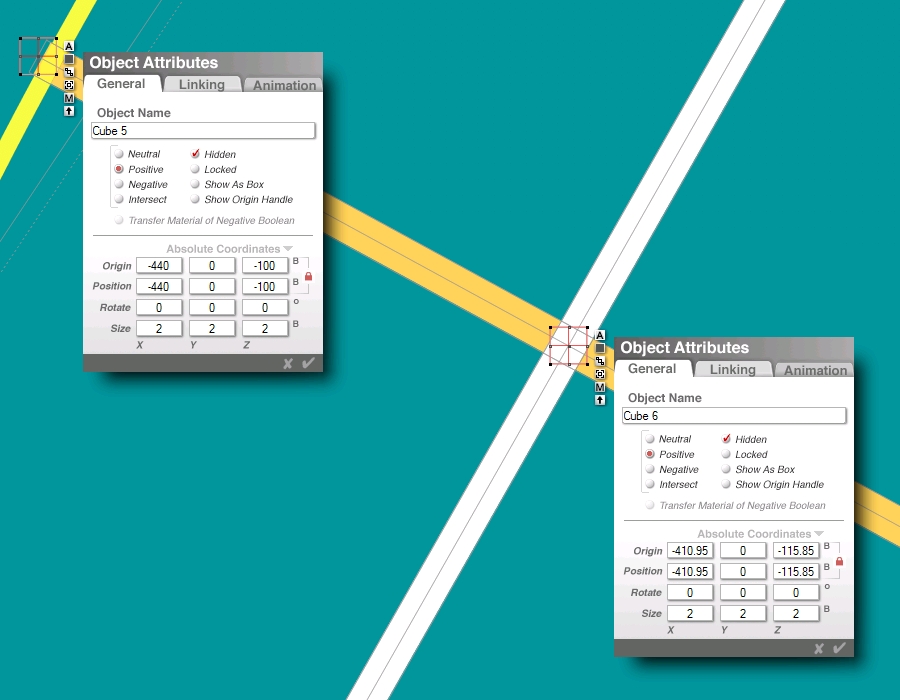
Astra - Giza - G1 South

G1 South

in rechecking measurements data
...before i went any further...
i noticed this neato little arc
...which i'll call: aG1sw250...
centered on the SW corner of G1
and given a 250 cubit radius...

and here's the link for that page again:
http://goodfelloweb.com/giza/jlpamp.html

(click pic for hi-rez)

south point intersects the G2 north line (G2n): given, radius of 250 cubits
west point intersects the G1 south line (G1s): at the grand plan hypotenuse
(aka GPH, running from G1nw to G3sw, and passing through G2sw along the way)

aG1sw also intersects LL exactly south of G1 center: at coordinates (0,-340)
as: 440/2=220; 220+120=340; *-1 ...or: -(440/2) -120 = -340 (from G1 center)

zooming in on the 120c box, centered south of G1
i thought it looked like the arc crossed line G1s
about halfway, and i was right, it bisects exactly

so, i threw in the half-square hypotenuse (cyan)
and just adjusted the angle, and length, manually
until it matched up close enough with the corners

...here's a screenshot of the overhead pesepctive in wireframe mode...
(the coordinates are center of the object selected, relative to center)
(which, far as this virtual model, document is concerned, is G1 center)
the center point of the angle (Cube 1) is 30c east of the G1ns line...
60c south of the G1s line, or: 280c south of the G1ew line (220+60=280)

as you can see, the angle i came up with is 26.57�
therefore the angle at the point i call z = 63.43�

anyways...
A2 + B2 = C2
(120x120) + (60x60)
14,400 + 3600 = 18,000
C = square root of 18,000 = 134.164...

the rule for half squares is:
hypotenuse equals half root 5
so: A, our primary side = 120
root 5 (2.236...) / 2 = 1.118

120 * 1.118 = 134.16
Cube 1 length 134.18
close enough, but...

...i resized it, just now, and it looks fine...
looking at the pic, a little closer, it is over
...but, not even the thickness of that red line
(and i'll just leave the old one up, for that)

and now... playing with the numbers, a bit...

taking those two statements, together...
C = 300 divided by the square root of 5
C = square root of 18,000 = 134.164...
...combine to find: 18,000 / 300 = 60
...which is B, our alternate side...

C times the square root of 5 (2.236...) = 300
so... C = 300 divided by the square root of 5

twice the square root of 5
2 x (2.236...) = 4.472
300 * 4.472 = 1341.6

1341.6 - 1732   = -390.4
1341.6 - 1417.5 =  -75.9
 390.4 -   75.9 =  314.5

i wonder what those little arc defined triangles are
and i don't know who to ask what the formula would be
but borrowing some pseudo-lunar terms, for a minute...
it looks like the teal sliver equals the purple sliver
probably about the same as that little green sliver
...and it follows that the larger teal full-gibbous is
the sum of the other 2 larger purple triangular areas

put it up against the other
big numbers on the plan...

close to 100 times pi...
we'll keep it in mind...

n here's the view of all that, from the SE...
shows how thick and tall the objects are...
for the squares, i just used 2D planes...

(click pic for hi-rez)

http://en.wikipedia.org/wiki/Square_root_of_5

four 60c squares (green, red, blue, purple)
(left pair, further bisected: teal, violet)
marking a geometric area, between G1 and LL
of incrementally divided half-measurements:
 aG1sw (yellow) the arc from G1's SW corner
 aG1sw radius = 250 cubits = 500c diameter
 half square = 60 x 30 cubits
 two square = 60 x 120 cubits
 S1 radius = 280, G1's height
 G1 sides = 440 (+60=500) aha
 LL - G1 = 120 (+280=400) hmm

LL - G1 hypotenuse (sky blue)
300 over the square root of 5
134.1640786499873817845504...
or, the square root of 18,000

 5 of those 60 cubit squares = 300
 their area (each 60c) 60x60=3600
 all 5 together add up to 18,000

so... 60 cubits... seems to have
a kinda significant proportional
relationship to the layout of G1

...the sides of G1... over 2...
the distance between G1 center...
and... any outer wall, laterally...
plus one of those 60 cubit squares...
equals the height of the great pyramid
thus, functionally: (G1s/2) + 60c = G1h
or, put expressively: 220c + 60c = 280c
...as this is the radius for the sphere

the area of G1: (440x440) = 193,600
over 40 = 4840, a nice round number
over 40 = 121, which is 11 squared
...area of G1 = (40x40) x (11x11)
a G1 side: 440 = 11 times 40
so there are 11 40c lengths
in the sides of the base
60 / 11 = 5.4545454...
transcendental number
theoretically, maybe
pi is transcendental

area of S1 (radius 280)
= pi times 280 squared
= pi times 78,400
= 246,300

describing the green wedges from before:
right triangle, with a curved hypotenuse
lines ABC (white), and points xyz (cyan)

the sharp point (x), coordinates (0,-280)
(measured from the G1 center point), marks:
- 60 cubits south of the G1 south edge (G1s)
- 60 cubits north of LL, halfway between them
- intersection of S1 and the G1 center NS line 
...so the radius of the sphere and height of G1

back wit me lil cubit rod
...different perspectives
...zooming in, looks like
...6.5 exactly...
...interesting...

reminds me of 130
from that big box between
the G1SW and G2NE corners

again, with geometry
right triangle rules
... A2 + B2 = C2 ...
(60x60)+(6.5x6.5)=3642.25
i get 60.3510563... for C

but it's an arc, actually
so anyways, still theory

that 0.35 difference from 60
35 = 7 x 5... (staggering 6)

ultra zoom, now: without elevating anything
the little gray squares are 10ths of cubits 
(and each difference in elevation is: 0.01)

round it off
...say it's 6
...6 x 60 = 360
degrees in a circle
almost days in a year
half of 720, twice 180
...180... three 60s...

three 60c boxes, west of center
leaves 40 cubits to G1sw corner

put in another 60c square
(yellow) (ok, n two more)
and measure that new side
and it's 27 (three cubed)

submitted for yer approval
consider a right triangle
. with sides: 120 and 27
. 120 = (60x2) = (40x3)
. 27 = 3 cubed (3x3x3)
. also: 3 from (3x10)

hypotenuse: A2 + B2 = C2
C2 = (27x27) x (120x120)
...729 + 14,400 = 15,129
...square root of 15,129
= 123, or 121 + 2
11 squared plus 2

729 x 14,400 = 10,497,600
root of 10,497,600 = 3240
= 81 x 40, or 9 x 9 x 40
or 3 x 3 x 3 x 3 x 40
3 to the 4th power
...times 40
(2x2x2x5)

...so, it's... pi...
....proportional....

a pyramid is a 5 sided 3-dimensional object
the volume of a square pyramid is basically
...side squared... times height...over 3...
one third that of a cube with the same base 
external zone equalling twice internal zone

the volume of a 60 cube = 216,000
that volume divided by 3 = 72,000
60 pyramid: (base, height each 60)
has a volume of: 72,000c... cubed
 2(11x11)=242; -216=26 ...twice 13
 (11 squared and double 13 balance)
so in theory: 60 is straddling 12
the average of those 2 prominents

while the right side of this webpage
is calculating the logical end of it
or, is attempting to make some sense
(without even a proper decoder ring)
let's go back, to the center square,
and have look at that right triangle
implied by... aG1sw-G1 intersection:

a 345 right triangle
27 side being the 3
(multiplying by 9)
the 4 would be 36
(6 10ths of 60c)
and: the 5 is 45
(7.5 10ths 60c)
(thus 15 20ths)
...4 and 5: are
being stretched
to 120 n 123...
becoming closer
...as they reach
out into infinity
(13 1/3):(13 2/3)
(ratio now 40:41)

and, the theoretical volume of G1:
. . . 440 x 440 x 280 = 54,208,000
. . . / 3 = 18,069,333 and a third
round up to 18.07 million: (x10^6)
...liking 18, 180, 7, 3 and curves

...and getting lost in the math...
but take that real number fraction
. . . . . . . times 3 = 54,208,000
...60 / 1.111... = 54.0000000...54
...54 = (6x9) = (2x27) = (2x3x3x3)
so we're close enough to something

more fun with G1 volume numbers...
 add em . . 440 + 280 = .. 193,880
 area / . . 440 x 280 = .. 123,200
 difference . . . --- = ... 70,600

and so... that's their relationship
break it down to common denomiators

two 30x60... half squares
...in purple and teal...
quad square... 30 x 120
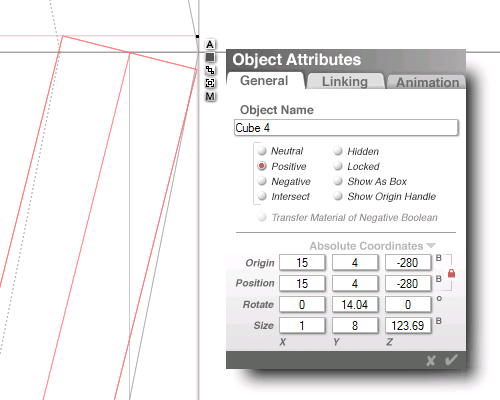
our new C side in pink

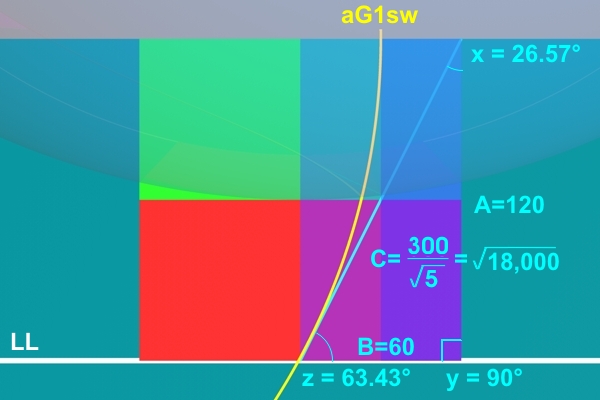
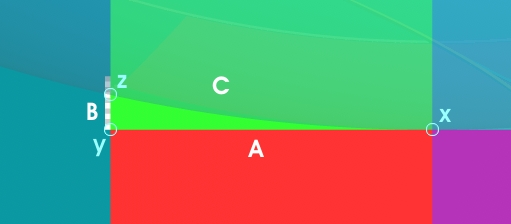
A2 + B2 = C2
(30)2 + (120)2 = C2
900 + 14,400 = 15,300
square root of 15,300
= 123.693168768529...
about 0.7 longer than our last one
about a half a percent difference
0.005635518443331841419856062...
about one 200th... or, 2x2x2x5x5
one over 2 cubed times 5 squared

the new hypotenuse (pink)
defines a chord on a G1sw
the midpoint: (naturally)
halfway between LL n G1s:
...but also very close to
the disk or edge of S1...

i could go in and measure
with a pair of objects...
...by exactly how much...
but we can tell from here
it's within about a cubit

and anyways, the real pyramids
aren't a "perfect" 90� exactly
(for strange, complex reasons)
so, not precisely 440c lengths
(which i'll investigate later)
but they're very very close...
so this is just a theory model
...starting with the basics...

back into wireframe mode:
shows this new hypotenuse
correctly measures 123.69
...at 14.04� clockwise...
...15.6 percent of 90�...
(3.9 percent of a circle)
93.6 percent of a 24th...
xx26ths; 3.9 x 51 = 99.45
so: 13 being an extension

...above, you can see the thickness is one cubit (8c tall)...
...below, i've temporarily thinned the lines to: 0.2 cubit...
(the actual line being their center, with easy 0.1 reckoning)
and introduced a 1 cubit diameter dot at coordinates (0,-340)

orange line: new angle from G1sw
measuring about: 250.6 at 61.39�
G1sw (-220, -220) ...to (0,-340)
with a midpoint of: (-110, -280)
(the height of G1 and S1 radius)

...and earlier C square angles...
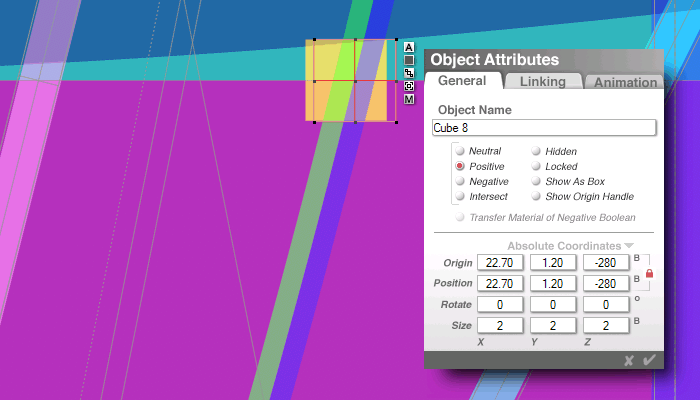
pink line = "Cube 4" (from above)
the cyan line is the angle
from the previous page (30, -280)
length of root 18,000 (134.16)

yellow line = arc aG1sw
...250 radius from G1sw
approximately 0.6 from:

green dot: focal point (0,-340)
340 cubits S of G1 center point
120 cubits S of G1 south edge..

the 250 cubit distance
from center point G1sw
is at the arc, exactly
the extra .6 cubits...

is: half the .2 cubit thick yellow line
plus half the 1 cubit diameter green dot
due south of G1 center point 340 cubits
and south of G1 south edge 120 cubits

and this arc continues further NNE to intersect G1s at (30, -220)

first of all:
(440:280) = (44:28) = (11:7)
internal adjacent primes to 6 n 12
280 is 63.636363... percent of 440
(7x9) step down, repeat infinitely
...7 and 9 stagger 8...
the mid-curve of 6 n 12
(7x40)>> 70: 2/3, 1/3, 2/3, 1/3...
defining a natural shape
with an artificial line
...so the actuality is
...just a guideline...
...and it's not really
appreciable in base 10
10 is here cuzza 2 n 5

1109.42857142857142857142857142...

...computer...?...
how did i just arrive at this number ?
...no response...
...ok...

1109.428571 428571 428571 428571..

123200 / 1109.428571___...
=111.0481586402266288951841359782

1109.428571 428571 428571 428571__
/ 280 (height of G1 and S1 radius)
= 3.962244897959183673469387755...
= 0.04... short of 4, or 2 squared

but, if instead of 100 for percent
we do 1000ths (so... per-milli...)
110.94285... so, just short of 111
...and then, it wants a smaller 60
then, it's an even smaller 30 over
...see how the numbers are making
little pyramid shapes themselves

111/280
0.39642857142857142857142857142857
reciprocal
2.5225225225225225225225225225225

111/440
0.25227272727272727272727272727273
reciprocal
3.963963963963963963963963963964

1109.4285714...
x 280 = 310,640

1109... / 440
2.52142857142857142857142857140...
5 halfs or 5 squared over 10 (2x5)
within a: "magnetic" range of that

 base area: 440 x 440 = .. 193,600
 vol: 440 x 440 x 280 = 54,208,000
. . . / 3 = 18,069,333 and a third
. 60 / 1.111... = 54.00000000...54

remembering the significance of 60
...and reaching... 54 is 6 from 60

squared about 3000 million million
 . . . . . . 2,938,507,264,000,000
60 short of 3000 (million million)
(or close enough to pay attention)

and cubed, it's:
 . 159,290,601,766,912,000,000,000
so about 16 and a buncha zeroes...
16 being 4 squared, (also 2 cubed)
and not an insignificant number...

70,600 / 440
= 160.45454545...

70,600 / 280 = 252.142857142857...
25 is 5 squared, n then pi minus 1
also: square root 2 plus 1 (or so)
and the difference we can make up:
by continually adding, subtracting
different various "sacred" numbers
ever closer in fractal progression
it's balanced, is what it's saying
and it seems like hogwash
except it's incremental

706 / 60 = 
11.766666666666666666666666...
from 12: a 2 or a 3 for staggering
and then thirds...

123,200 / 70,600 =
1.745042492917847025495750...
1.75 about, or seven eighths
which is: one eighth from 2

90 / phi (1.618...)
= 55.62422744128553770086526576...

500 x 400 = 200,000
...close to 180,000
(18,000 times 10)

180K is 20K less than 200K
it is 0.9 of (or times 9/10)
500 + 400 = 900
900 x 200 = 180,000

500 / 400 = 1.25
400 / 500 = 0.8

900 / 1000 = 0.9
9/8 = 1.125
8/9 = 0.888...

18/4 = 4.5
the average of 4 and 5

the average of 4x4 and 5x5 = 20.5
20.5 - 18 = 3.5

4.5 - 3.5 = 1
so there is one cubit
"straddling" numeral 4
that's our area of operation

...and, rounding off to the nearest nice round
"social" (and perhaps non-prime) whole numbers
(gravitating with preference to a commonality)
...18 is the (adjusted) average of (37/2)
...the average of (4x4) and (5x5) = 20.5

16 + 25 = 41
41 / 18 = 2.277...
add that to phi
(2.277...) + (1.618...) = 3.89581...
almost 4

ok, times phi
(2.277...) x (1.618...) = 3.68531...
from 4 is 0.3146814

-3.146814...
reminded of pi and phi/10

the square root of 1,800,000
= 1341.640...

that means
the square root of 1,800,000 equals:
300 times twice root 5 (4.472...)

300 times twice root 5 (4.472...)
300 * 4.472 = 1341.6 from before

i still want to put it up against
the other big numbers on the plan
1341.6 - 1732 = -390.4
1341.6 - 1417.5 = -75.9
390.4 - 75.9 = 314.5
close to 100 times pi
we'll keep it in mind

0.818...

500 x 400 = 200,000
and the square root of 200,000 
= 447.21359549995793928183473374626

ok, so... the square root of 200,000
= 447.213595499957939281834733746...
...close to 440 G1s... 7.2135... off
21=(7x3) and 35=(7x5)... (stagger 4)

closer is the square root of 180,000
(10 times the square root of 18,000)
= 424.264068711928514640506617262...

...the difference between them is...
22.949526788029424641328116483346...
their ratio is 8:9

again, square root of 5
is ... 2.236067977499789696409173...
x10 = 22.360679774997896964091736...
a difference of:
...... 0.588847013031527677236379...

...radial pixelization
...expressing a curve,
with geometric shapes:
as any regular polygon
expresses a circle...

with accuracy depending on the resolution...
just as with phi: (2:3, 3:5, 5:8, 8:11...)...
the higher up the Fibonaci sequence you go...
the more accurate the ratio is represented...
http://en.wikipedia.org/wiki/Fibbonaci_Series

that same approximately 60� angle from G1sw
...on the opposite side of the circle aG1sw

...bisects the chord created by
GPH (between G1nw and G3sw)...

(click pic for hi-rez)

so, now we have another, larger right triangle to measure
between our green focal (0,-340), G1sw corner (-220,-220)
and our new right angle corner, on LL (-220,-340)
A = long side: (EW) = 220 (G1s/2); (60x3)+40
B = short side: (NS) = 120 (G1s-LL); (60x2)
C = hypotenuse... go to the blackboard....

A2 + B2 = C2
(220x220) + (120x120) = 
48,400 + 14,400 = 62,800
...and square root of 62,800 =
250.59928172283335576990729631506
250.6
which we already knew from observing
but it's always nice to verify figures

without even going into the program and measuring
i can tell that the opposite corner is (-440,-100)
(G1s/2)x2 = (-220x2=-440) = the length of a G1 side
(G1ns/2)+120c-(2x120c); (340-240=100); (220-120=100)

the angles i actually have for those objects
are 61.39� and -60.38� (zoom eyeball range)
but, then... i'm not doing it exact, yet...
maybe there's something to that extra 0.4�

and: comparing to the G1sw-G2ne semi-square (green box)
so, it doesn't line up exactly with G2e (-220-215=-435)
but it's only 5c off, so we'll not discount it entirely

let's have a look at that chord
(defined by the white GPH line)
and reflect it back to SE of G1

first, what would those coordinates be ?
eyeball estimate of: (-410.95, -115.85)
 reflected off of G1sw: (-220, -220)
...so, differences of: 190.95, -104.15
 just add that to G1sw: (-220, -220)
...new object center: (-29.05, -324.15)
...and it's about 240c at 30� rotation
nice round numbers 250c radius circle

it's a hexagon: aG1sw forms a hex

and i'm not gonna do it right now
we'll see if it's also a 12 sided
or a 24 polygon or whatever later
but, real quick, here's a mockup

again, the green angle is not exact
but it's within about a cubit or so

...and another...

that odd square bG1sw-G2ne (213x250) = 50 : 42.6
if just 2 cubits wider, at 215 it'd be 50 : 43
very close to hexagonal proportions of 50 : 43.3
...or 2 : the square root of 3 (1.7320508075...)
(20:17.32) (30:25.98) (40:34.64) (60:51.96) ...

half root 3 (0.866...) times 250 = 216.506...
 1 / root 3 (0.577...) times  60 =  34.64...

http://en.wikipedia.org/wiki/Square_root_of_5

if that red square is 60:
the radius of gray circle
is half root 5 (1.118...)
 ...times 60 = 67.082...
 (diameter of 134.164...)
so 134.16 and centered at
30 cubits east or west...

3 equilateral triangles...
with sides, that radius...
60 (root 5)/2 = 67.0820...
(yellow line is drawn on)
...that wide green line...
is the opposite chord, to:
aG1sw250 of GPH, G1nw-G3sw
(grand plan hypotenuse)...

...a hexagon with long width
(point to pont) of 134.16...
(which is: 120 x half root 5)
fitting inside the new circle
centered where aG1sw enters G1
(at coords: 30 east, 220 south)
...is demonstrating a kind of..
cooperative geometric harmony...
and a method to the proportions..
but doubled and centered on G1s...
fits the square in the center half
...curve crossing on LL (340 south)
120 cubits from the south edge of G1

just for clarification
the orange line is the
hypotenuse of G1sw and
the green dot point...
aka: G1ns-LL (0, -340)
so, angle: G1sw-G1nsLL
turned 28.61� rotation
length of 250.6 cubits

the yellow line is the
30/60� angle from G1sw

extending the hexangle
to the G1 center line:
takes another 4 cubits
(254 radius, 508 diam)
...at coords (0, -347)
4 and 7 cubits exactly
...the green square...
seems to be... a point
of particular interest
even some significance

the midpoint line between
G1s (-220) and G2n (-470)
...250 cubits... total...
(250/2=125) (125+220=345)
so... 345 cubits south of
the G1 center line (0, 0)
so, the green box is just
2 cubits south of that...

(click pic for hi-rez)

...one last thing, about these angles...
the yellow square is 22.5 east of center
exactly halfway between the other angles
(or, 3/4 across the half square's width)
...purple and blue, discussed earlier...
...(purple crosses at 15, blue at 30)...
the 250 cubit arc (from the G1sw corner)
passes right through it (almost exactly)
the actual crossing is about 22.7 cubits

so, the curve of aG1sw250
spans 3/4 the short width
and 1/2 the longer height
...of this exact specific
half-half-square (30x120)
with only a tiny .2 cubit
difference (east to west)
...but, this is going off
ideal design measurements
...the real monuments are
off by about that much...
here and there, for other
strange, complex reasons

Giza

G1 South

� prev �
Layout

� next �
G1/G2 Square