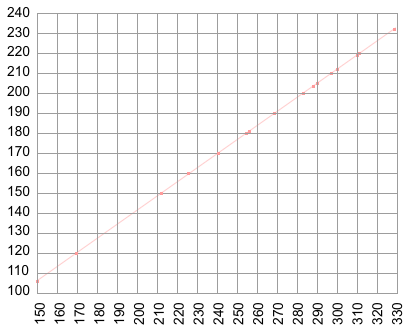
the 2 main pyramids, G1 and G2
are offset, slightly, from 45�
by an odd rectangle measuring:
...213 cubits by 250 cubits...
|
...a proportion of: 50 to 42.6
or one to 1.173708920187793...
or opposite reciprocated (1/x)
= one to 0.852 even... hmm,,,
0.852 / 213 = 0.004 exactly...
...4 thousandths of a cubit...
now, that is something special
|
|
|
 |
|
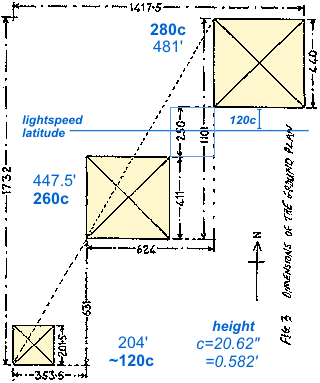
...blue shaded area
hereby dubbed bG1G2
for the box between
the SW corner of G1
and NE corner of G2
measures 250 cubits
..north to south...
n an odd 213 cubits
...east to west....
.... 250 x 213 ....
53,250 cubit square
|
|
|
LL crosses right through it, almost halfway...
dividing it into two rectangles of 120 and 130
|
|
|
120 x 213 = 25,560 square cubits
130 x 213 = 27,690 square cubits
total area = 53,250 square cubits
half areas = 12,780 and 13,845
50,000 + 3,250 = 52,000 + 1,250
50K + (13x250) = (13x4K) + (5x250)
250 = (25x10) = (5x50) = (50x10)/2
250 = (5x5x5)x2 = 5 cubed, times 2
13 = (5x2)+3; (7 from 20)
and the 5th prime number
...not counting 1 and 2
anyways, 5 and 2 are 7
stagger 6 for 2 and 3
|
|
|
|
|
...what geometry might we derive is implied, here ?
for example... the center triangle's height is 5...
but what are the other measurements... angles etc ?
...i'm reminded of a pentagram... but it's squashed
...or, maybe a hexagon... close, but not exactly...
|
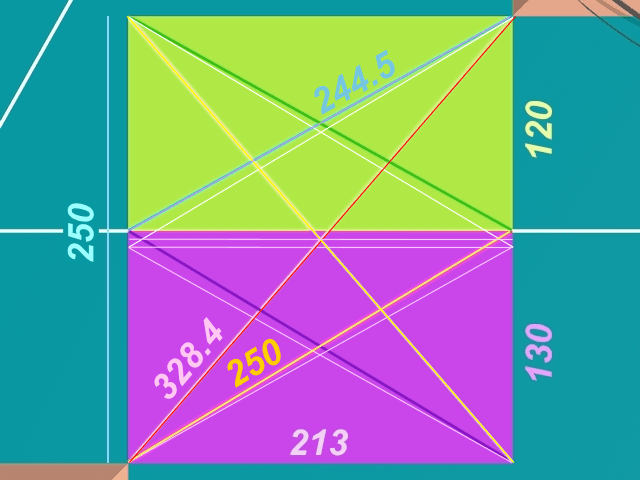
entire section: a2+b2=c2
red and yellow angles
(213x213) + (250+250)
45,369 + 62,500 = 107,869
c = 328.43416387458841...
|
|
|
 |
|
north section: a2+b2=c2
blue and green angles
(213x213) + (120x120)
45,369 + 14,400 = 59,769
c = 244.4769927825520...
|
south section: a2+b2=c2
violet and orange angles
(213x213) + (130x130)
45,369 + 16,900 = 62,269
c = 249.5375723212839...
|
|
|
 |
|
|
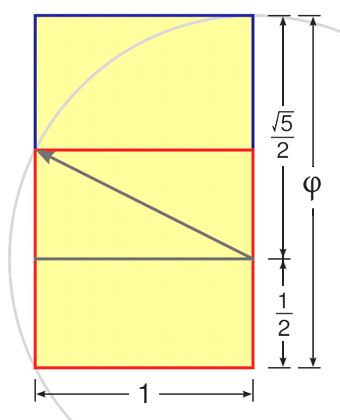
the red square above = 1 by 1
the angle for the half square
is half root 5... or 1.118...
|
now make a rectangle
with that for a side
and 1 for the other:
|
|
|
|
|
Don Barone:
213 divided by 250 = 0.852
sine 0.852 = 58.43 degrees
reciprocal (90-58.43) = 31.57
...sine 31.57 is 0.5235418...
nothing special... HOWEVER...
close to golden ratio, phi is
tan of 31.57 = 0.61448566...
and the angle we need to get
exactly phi... 0.618033988...
= 31.717474380370653213260...
...so, taking this from 90...
= 58.282525619629346786739...
and sine of this, gives us...
= 0.850650808637316884920...
and, multiplying this by 250:
= 212.66270215932922123010...
0.33 cubits... about 7 inches
...but the 250 IS NOT EXACT !
it would appear that Phi seems
to be hidden here in this offset
for the distance IS NOT EXACTLY 250
it could be that it works out EXACTLY
and that the angles of this rectangle
are EXACTLY 58.2825... and 31.71747..
A GOLDEN RECTANGLE !!!!!!!
Very, very interesting !!!
|
|
|
the square root of 5 is: 2.236...
thus, half of root 5 is: 1.118...
...so, the ratio is 1 to 1.118...
plus one half: (1/2) (0.5) is phi
the golden ratio: one to 1.618...
or, reciprocated: one to 0.618...
see how that works... this number
|
|
|
but... the ratio of 250:213
is small side to 1.173.....
or large side to 0.852 even
|
|
|
0.852 / 213 = 0.004
times 1000 = 4
250 / 1000 = 0.25
|
|
|
|
|
these ratios are found everywhere in nature...
seashells, flower petals, faces and fingers...
but in practice, curves don't change abruptly:
it's more of a gradually adjusting inclination.
so, the average arc for each section is correct,
and the sides touch, but there's no sudden shift
so our alignments will be a bit off now and then
but it's representative... reflective, of nature
|
|
|
expressed simply in the Fibonacci sequence...
...adding the last 2 numbers to get the next...
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ... etc...
3:5, 5:8, 8:13, 13:21, 21:34, 34:55, 55:89 89:144
(the higher up you go, the more accurate you get)
...and... notice the little pyramid triangles...
|
|
|
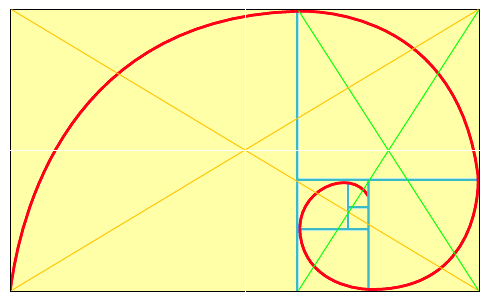 |
...basically... the proportions of the
small section to large section, equals
large section to total... and so on...
|
|
|
the box between G1 and G2:
is comparing the distances
... 250 and 213 cubits ...
|
|
|  |
|
interlocking circles
reminds me of vesica
|
|
|
and, of course, these 250 cubit arcs
...don't align to vesica... for that,
their shared radius would have to be:
...the distance from their centers...
the hypotenuse of the rectangle bG1G2
|
|
|
|
 |
the idea behind a vesica is that: 2 circles share the same radius, in common
|
|
|
 |
remembering from before...
that distance is 328.43...
|
half of that is 164.215...
100 + 64 = (60+40) + (8x8)
= (2.3.5.2) plus (2.2.2.5)
plus... 2 to the 6th power
|
|
|
...but see how close, the...
...center vertical of the...
rough overlay vesica (below)
(same 250 cubit radius arc)
conforms to a side of G1...
(checking the math on that)
...radius times... root 3...
/3 x 250 = 433.0127018922...
just less than 7 cubits less
|
|
|
it might strangely work
for G2 also, somehow...
433 is 3 times over 400
what G2 side is, at 411
(11x3=33); and then a 7
...that brings us to 40
G1 down to 400, with G2
|
|
|
|
 |
i also like that equaliateral triangle
(sides same as the radius, 250 cubits)
marking a chord on aG1sw, intersecting
GPH (grand plan hypotenuse): G1nw-G3sw
|
and, here, giving aG1sw a
vesica clone to the west:
they too intersect at GPH
(green-yellow diagonal)
|
and a couple other
points of interest
that pop right out
(circled, below)...
|
|
|
 |
...the lower left circle...
was zoomed in on earlier...
aG1sw-aG2ne (-470, -222.75)
|
the image below is a zoom
of the upper circle point
...in the image above...
|
...and the lower right circle
...south G1 center (30, -220)
is discussed on the next page
|
|
|
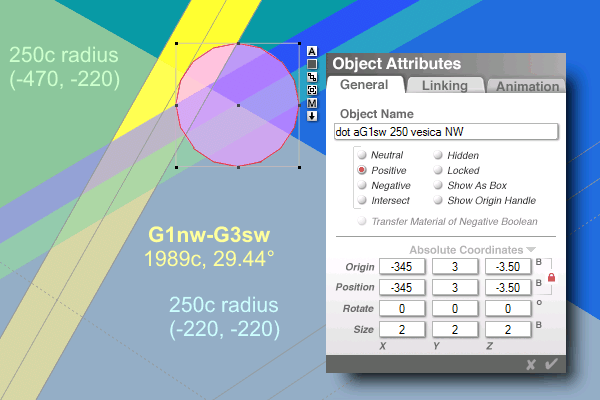 |
it seems to me, that 29.44�
if made, to be an even 30�
taking into consideration
...that the base of G1...
is significantly lower...
than the rest of the plan...
...like... 30 cubits, or so...
i don't recall exactly, and it's
information i don't have handy...
(just putting the idea out there)
keep it in mind for spheres later
|
|
|
|